概念
回归(Regression)是指确定自变量和因变量之间的相互关系。线性回归(Linear Regression)是指自变量和因变量之间的关系是线性的。
$$
h_{\theta}(x)={\theta}_0 + {\theta}_1x
$$
在这里,求${\theta}_0$和{\theta}_1x$即为线性回归求解。
上面那个例子中,自变量只有一个房价,实际可能存在多个自变量,那么线程回归就变为:
$$
h_{\theta}(x)={\theta}_0 + {\theta}_1x + {\theta}_2x + \cdots + {\theta}_nx
$$
这样表示有点麻烦,可以用矩阵表示:
$$
h_{\theta}(\textbf{x} )={\theta}^T{\textbf{x}}
$$
这里${\theta}$和$\textbf{x}$都是向量。显然用向量的形式表示更加简洁易懂。
代价函数(Cost Function)
当确定了一个线性关系后,怎么来确定${\theta}$的值呢?一个评价标准就是代价函数。代价函数用来描述$h_{\theta}(\textbf{x} )$和真实情况的差距。
假设只有一个变量$x$,即$h_{\theta}(x)={\theta}_0 + {\theta}_1x$。现在有样本$m$个,定义代价函数:
$$
J(\theta_0,\theta_1) =\frac{1}{2m}\sum_{i=1}^{m}\left( h_{\theta}(x^{(i)}) - y^{(i)} \right)^2
$$
代价函数的物理意义为真实值和预测值之间误差的平方和的均值,这里假设了共有$m$个样本。在求均值时还乘以了$\frac{1}{2}$,目的是为了便于求导。这是一个单变量的线性回归,当自变量为多个时,代价函数变为:
$$
J(\theta_0,\theta_1,\cdots,\theta_n) =\frac{1}{2m}\sum_{i=1}^{m}\left( h_{\theta}(x^{(i)}) -y^{(i)}\right)^2
$$
我们最终的目标为:
$$
min:{J(\theta_0, \theta_1, \cdots, \theta_n)}
$$
常用的一种发放为梯度下降法:
梯度下降法(Gradient Desent)
函数对某一变量求梯度,那么在梯度方向上,函数增长最快;同理在梯度负方向上,函数下降最快。梯度下降法就是在梯度的负方向上下降。
其大概思想为:随机初始化$({\theta_0, \theta_1, \cdots, \theta_n})$,之后计算代价函数。使用梯度,更新参数,寻找下一组能让梯度下降最多的参数组合;一直迭代,直到达到最大迭代次数或找到最优点(可能是局部最优)。
对于
$$
J(\theta_0, \theta_1, \cdots, \theta_n)
$$
求梯度:
$$
\frac{\partial J(\theta_0, \theta_1, \cdots, \theta_n)}{\partial \theta}
$$
因为$\theta_0$特殊,求导要区别开来:
当$j=0$时
$$\frac{\partial J(\theta)}{\partial \theta_j}
=\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}(x^{(i)}) - y^{(i)} \right)
$$
当$j \neq 0$时
$$\frac{\partial J(\theta)}{\partial \theta_j}
=\frac{1}{m}\sum_{i=1}^{m}\left( (h_{\theta}(x^{(i)}) - y^{(i)} )*x^{(i)}\right)
$$
算法流程为:
重复:
$$
\theta_0 := \theta_0 -\alpha\frac{1}{m}\sum_{i=1}^{m}\left( h_{\theta}(x^{(i)}) - y^{(i)} \right)
$$
$$
\theta_i := \theta_i -\alpha\frac{1}{m}\sum_{i=1}^{m}\left( (h_{\theta}(x^{(i)}) - y^{(i)} )*x^{(i)}\right)
$$
直到收敛或达到最大迭代次数。其中$\alpha$为步长,即为每“迈一步”要走多远。
在上面式子中可以看出,迭代更新一次,算法复杂度为O(mn)。m为样本个数,n为自变量个数。如果样本量比较大,更新一次梯度可能需要很久,这样的方法叫做批量梯度下降法(Batch Gradient Desent)。
还有一种更新梯度的方法:随机梯度下降法(Stochastic Gradient Desent)。其思想为,根据每一个样本,更新梯度。
for i = 1 to m
$$
\theta_0 := \theta_0 -\alpha\left( h_{\theta}(x^{(i)}) - y^{(i)} \right)\
\theta_i := \theta_i -\alpha\left( (h_{\theta}(x^{(i)}) - y^{(i)} )*x^{(i)}\right)
$$
两者区别
从上面的式子中,可以看出
(1)批梯度下降法为使所有样本的代价函数最小;而随机梯度下降法为使每一个样本的代价函数最小。
(2)批梯度下降法,每一步都是朝着全局最优点方向前进,而随机梯度下降法是大概朝着最优值方向前进。最后的结果可能是批梯度下降法找到最优点,而随机梯度下降法是在最优点附近徘徊。
特征缩放
如果训练样本的多个特征之间的“尺度”差别很大,那么需要对这些特征进行缩放。例如房子价格和其面积、房间个数的关系中,面积可能为几百平方,而房间个数可能为几个;几百与几个之间的度量差别很大。在最优化时,在不同方向上,前进的步长差别很大,很可能造成迭代很多次才能找到最优点。为了更好的使用这些特征,需要进行特征缩放:
$$
x_n = \frac{x_n - \mu_n}{s_n}
$$
其中$\mu$是均值,$s_n$是标准差。
特征缩放后,其均值为0,方差为1。
例子
参考stanford
参考stanford的练习
在这个例子中,只有一个变量,在程序中,可以假设存在$x_0=1$,这样便于编码。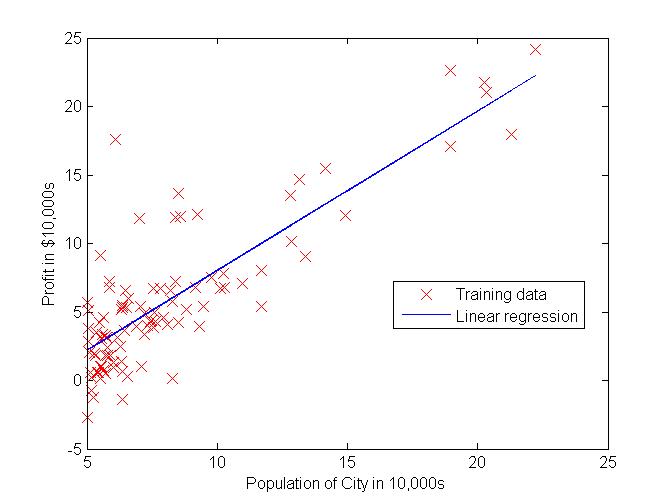
因为只有$\theta_0$和$\theta_1$,可以画出$J(\theta)$随这两个变量变化的3D图: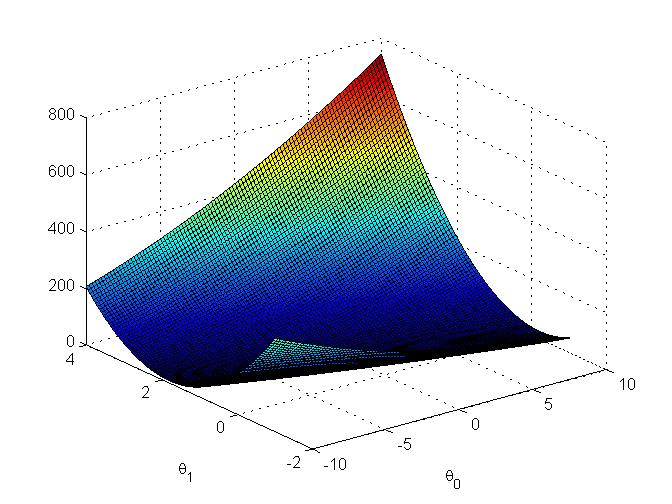
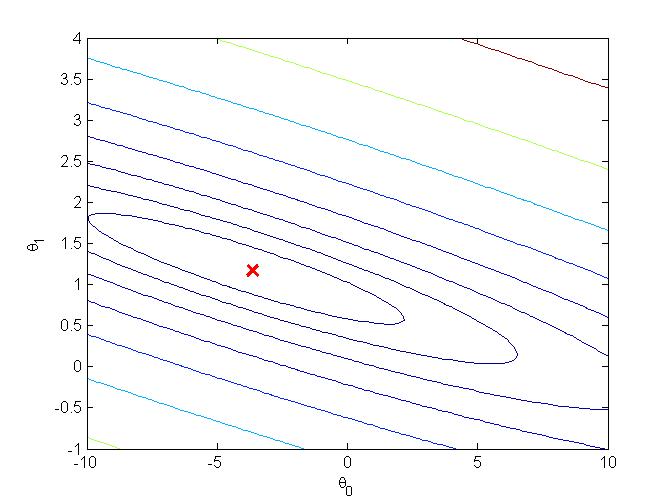
可以画出等高线,看一下最优点: