逻辑回归(Logistics Regression)
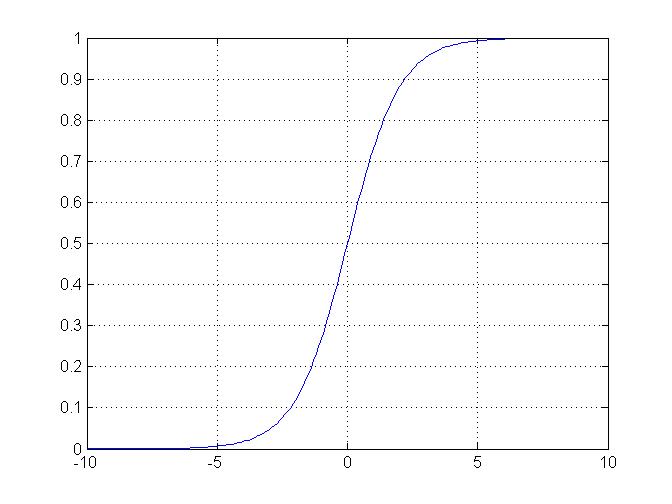
逻辑回归和线性回归类似。在现实回归中,函数$h_\theta(x)$是个线性函数。输入$x$和输出是线性关系,如果$x$很大或很小,那么输出范围难以控制。逻辑回归可以解决这个问题。逻辑回归把输出限定在了一个范围内,常常用于分类问题中。
逻辑回归,对于给定的输入值,输出都在$(0, 1)$之间。用于分类问题时,例如肿瘤大小和其是否是良性,这是个二元分类;可以分为0和1,对于输出给出一个阈值$\eta$,输出大于阈值阈值$\eta$时,判断为1,小于阈值$\eta$,判断为0。
决策边界(Decision Boundary)
假设
$$
h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)
$$
$\theta=[-3, 1, 1]$,当$-1+x_1+x_2>0$时,判断为1,否则为0。那么可以得到一个决策边界,如下图所示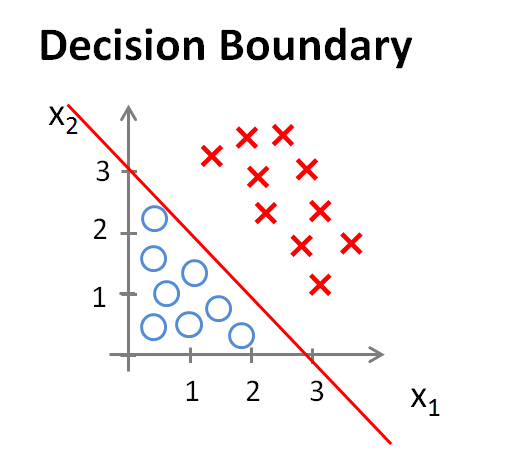
如果边界是非线性的呢?如下图所示: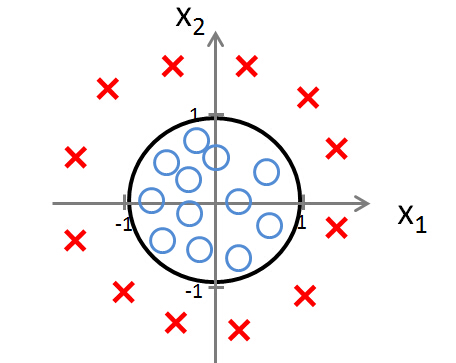
那么可以用一个高阶函数来拟合。
$$h_\theta(x)=g(\theta_0+\theta_1x_x+\theta_2x_2+\theta_3x_2^2+\theta_4x_2^2)
$$
这里$\mathbf\theta= [-1, 0, 0, 1, 1]$。当$-1+x_1^2+x_2^2>0$时为一类,否则为另一类。如果形状更为复杂,那么可以通过更复杂的高阶公式来拟合。
损失函数(Cost Function)
对于线性回归,损失函数的含义为:真实值和预测值之间误差的平方和均值。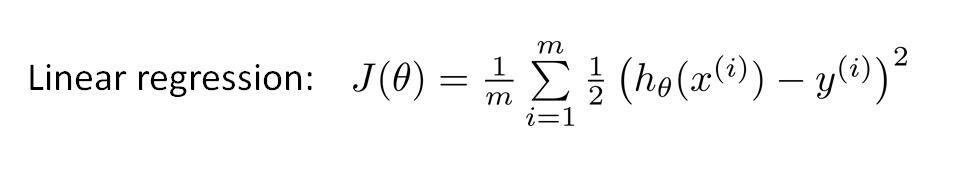
如果将逻辑回归的
$$
h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta x}}
$$
直接代入,得到的将是一个非凸函数。这样的代价函数有许多局部最小值,使用梯度下降法,可能找不到全局最优值。重新定义损失函数如下: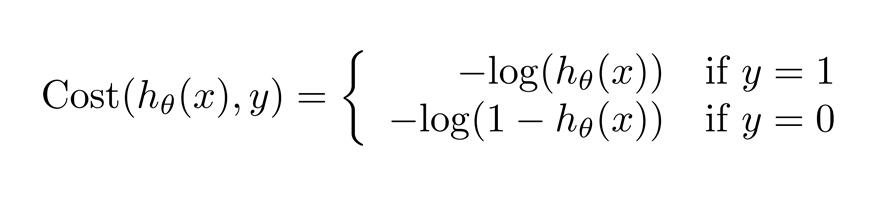
这样损失函数的意义就非常清楚了:
- 当$y=1$时,如果$h_\theta(x)$在$(0, 1)$区间上,离$1$越远,那么损失函数值$-log(h_\theta(x))$越大。
- 当$y=0$时,如果$h_\theta(x)$在$(0, 1)$区间上,离$0$越远,那么损失函数值$-log(1-h_\theta(x))$越大。
如下图所示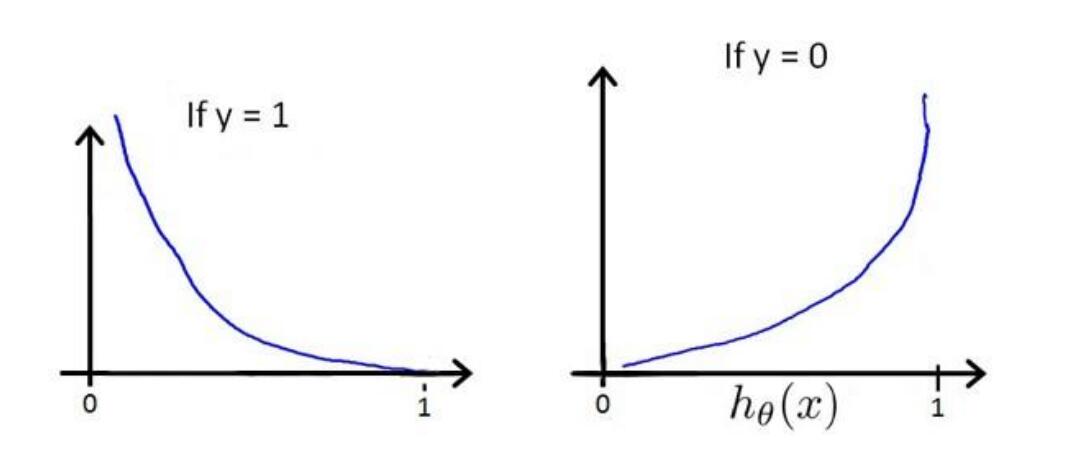
因为$y$总是0或1,损失函数可以推导为: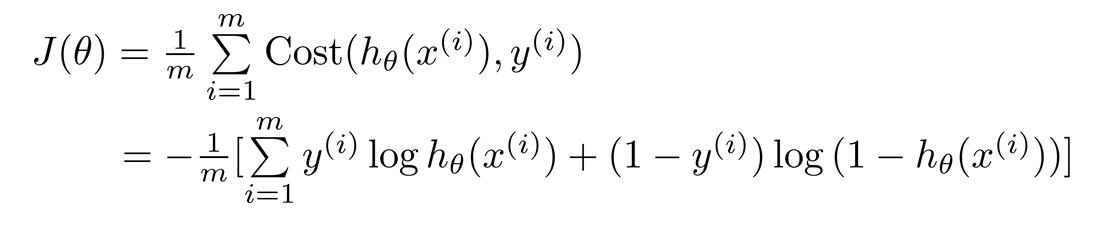
梯度下降
最小化损失函数$J(\theta)$,逻辑回归也是用梯度下降法。$h_\theta(x)$的含义为$y=1$的概率,对于输入$x$,$y=0$和$y=1$的概率为: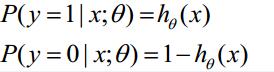
结合起来: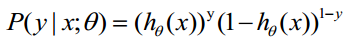
求最大似然函数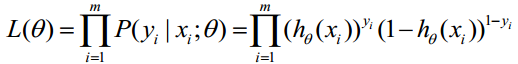
求对数最大似然函数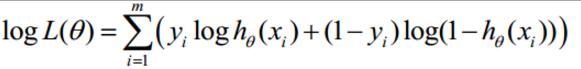
这个结果很像损失函数$J(\theta)$。
参数更新过程为: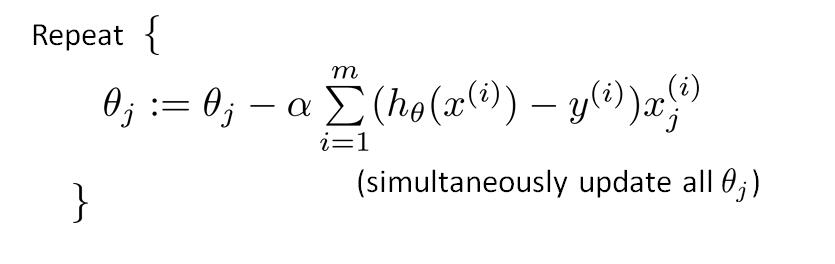
矩阵化
上面梯度更新的过程,需要一个for循环m次。可以用 矩阵的形式一次完成;下面$x$的每一行为一个训练样本,那么:
可以看出$h_\theta(x)-y$的m的循环,可以由$g(A)-y$一次完成。因此梯度为:
$$A=x\theta$$
$$E=g(A)-y$$
$$\theta:=\theta-\alpha x^TE$$
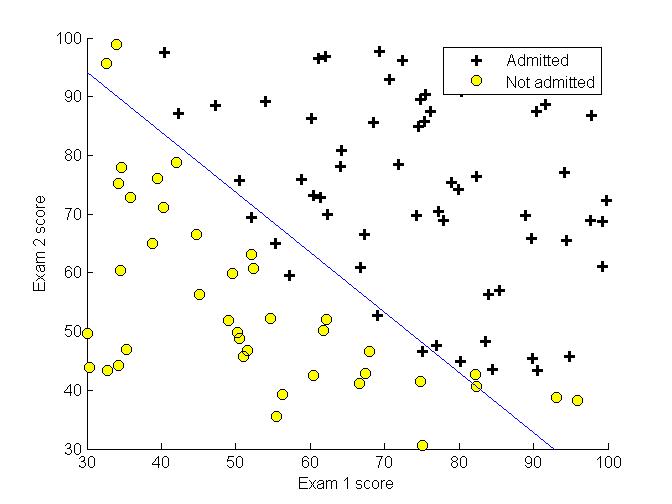
实验
训练数据为两门课的考试成绩,根据这两门课的成绩来决定是否录取。先可视化训练数据。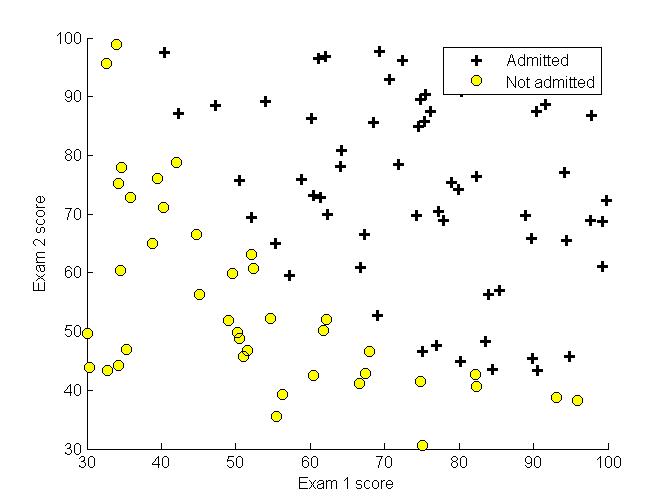
回归函数为
$$
h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta x}}
$$
损失函数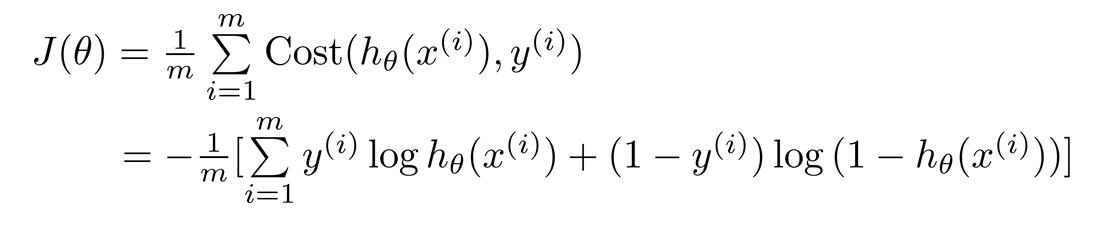
参数更新过程为: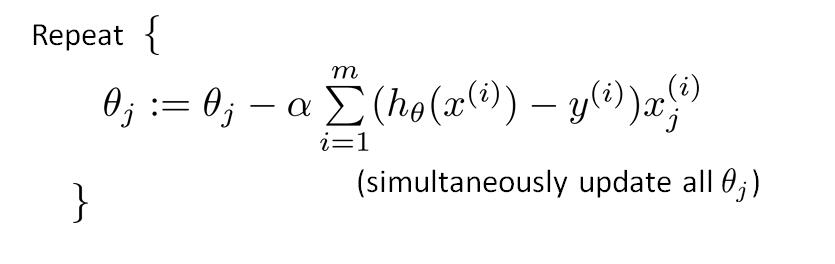
这里用到两个函数1
options = optimset('param1',value1,'param2',value2,...)
这个函数作用为创建一个最优化选项,设定参数的值。1
options = optimset('GradObj', 'on', 'MaxIter', 400);
表示使用梯度来优化目标函数,最大迭代次数为400次。fminunc用于求无约束最优化的最小值。这里用法为1
2[theta, cost] = ...
fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);
优化函数costFunction,优化的参数为t,其初始值为initial_theta,用到了上面创建的最优化选项。最有求得的结果,如下图