过拟合
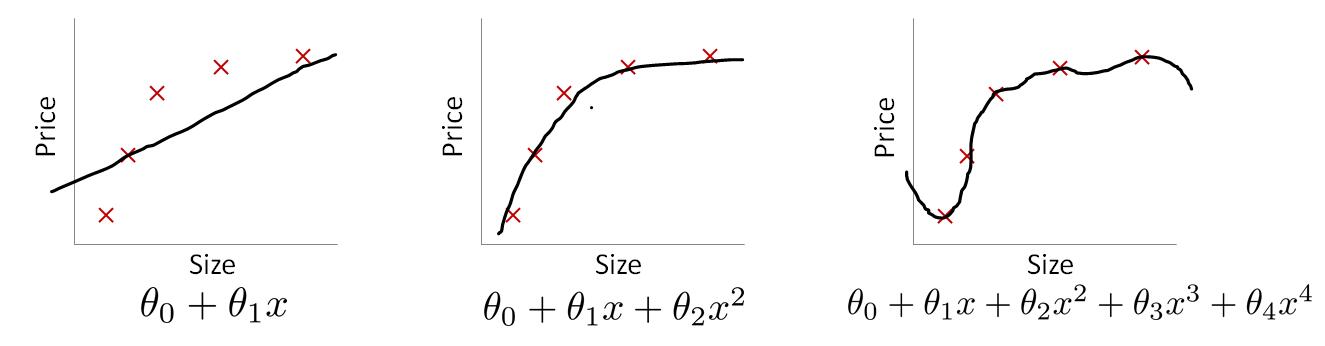
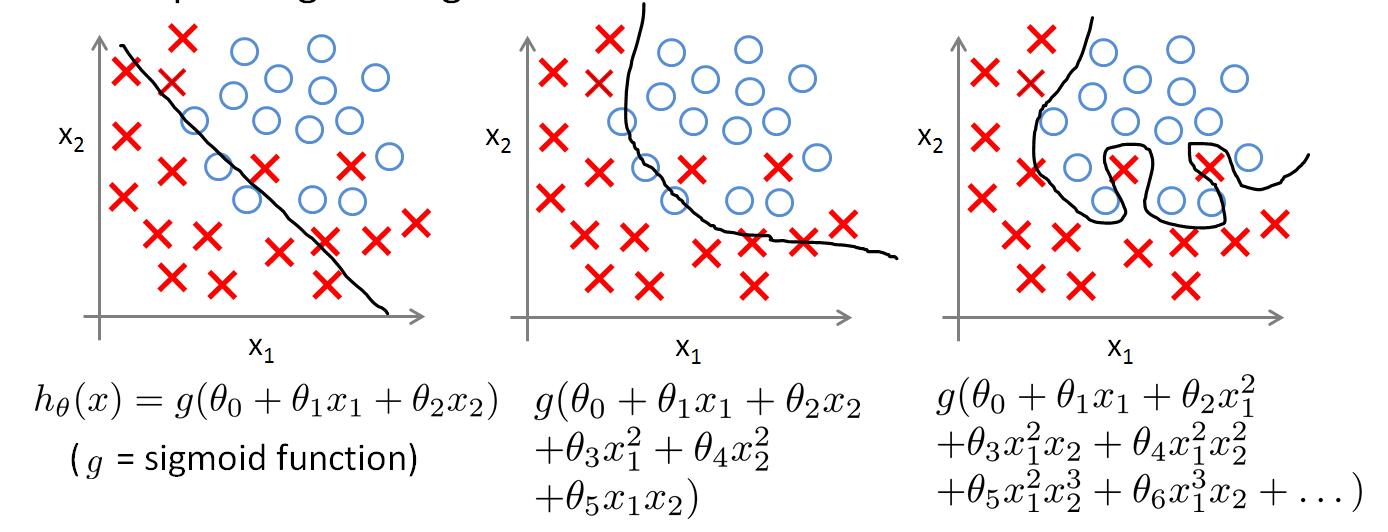
通过机器学习,得到的模型可以非常好的适应训练集,代价函数loss值接近0,在训练集上的准确率接近100%。但是如果扩展到训练集意外的数据,准确率有下降很多。这就是产生了过拟合现象。
当产生了过拟合时,可以通过以下方法解决:
- 抛弃一些训练使用的特征。或者使用模型选择算法。
- 正则化。保留所有的特征,但是可以通过参数$\theta_j$减少特征的影响。
代价函数
在线性回归过拟合的例子中,主要是因为高次幂特征的影响,产生了过拟合;减少这些特征的影响即可。它的回归模型为
$$
h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\theta_4x^4
$$
重新定义代价函数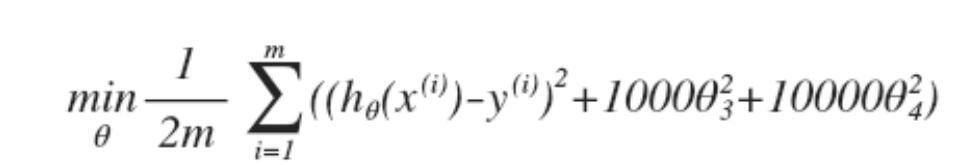
这样的话,参数$\theta_3$、$\theta_4$将非常小。高次幂的影响就非常小了。上面是对2个高次幂特征进行了惩罚。
如果要对所有参数$\theta$进行惩罚,一般通用的代价函数为: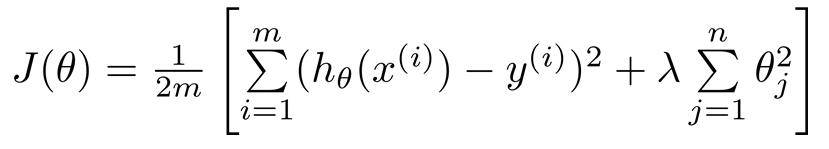
注意,不对$\theta_0$进行惩罚。$\lambda$叫做正则化参数(Regularization Parameter)。
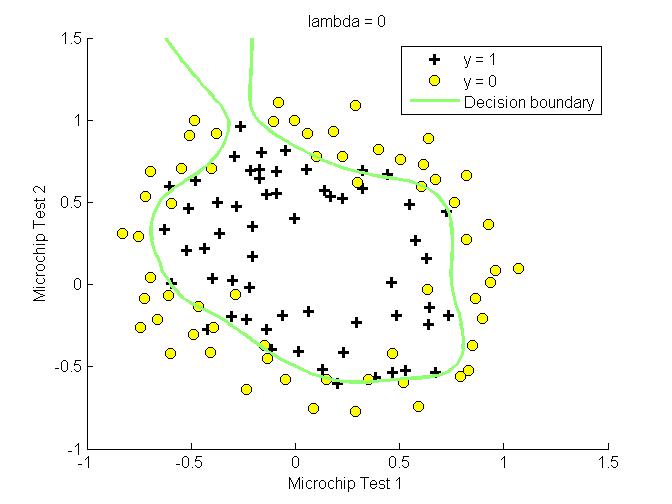
$\lambda$选取非常重要,如果太小,将没有太大影响;如果太大,造成$h_\theta(x)=\theta_0$,产生欠拟合。
正则化线性回归
线性回归,增加正则化后的代价函数为: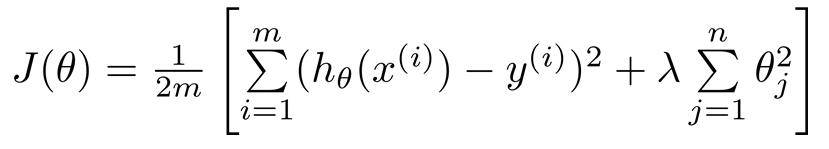
因为不对$\theta_0$进行正则化,所以梯度下降分2中情况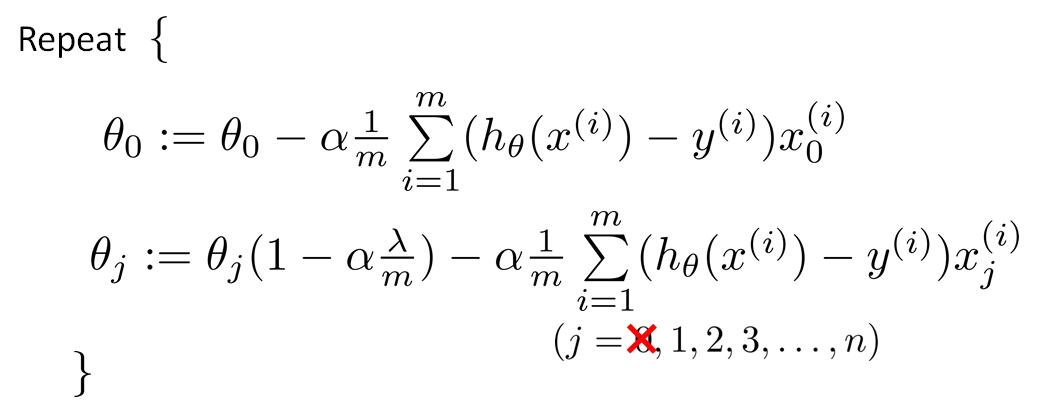
可以看出,增加正则化后,每次参数更新都比原来减小了一个值
正则化逻辑回归
对于逻辑回归,增加正则化后的代价函数为: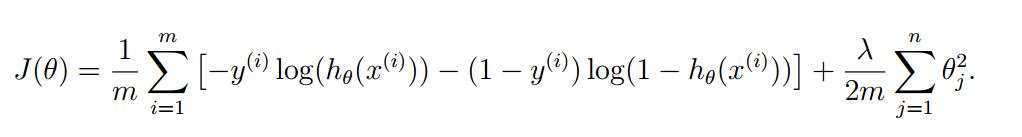
梯度下降过程为: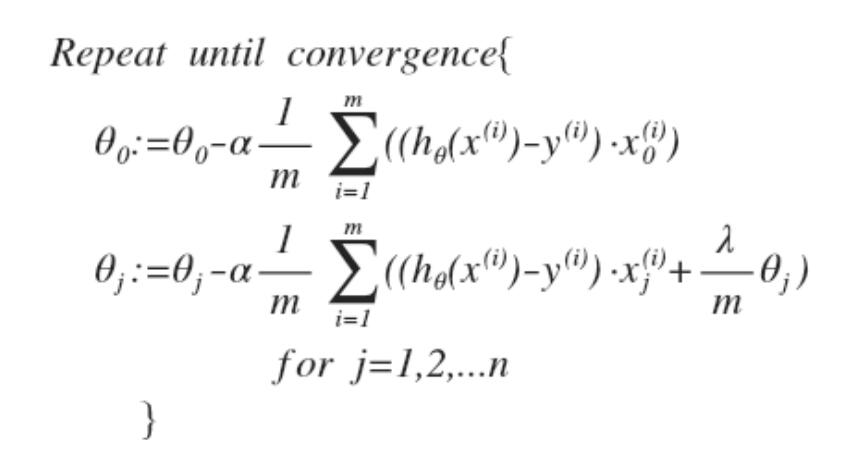
逻辑回归和线性回归的正则化梯度下降看上去类似,但是它们的$h_\theta(x)$,不同。
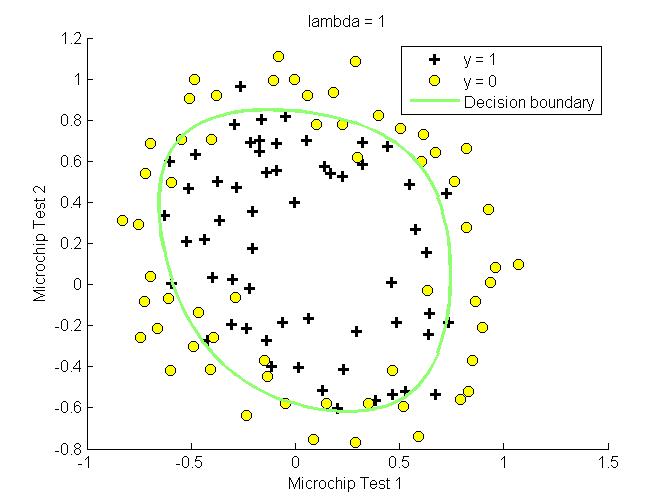
实验
首先画出样本分布图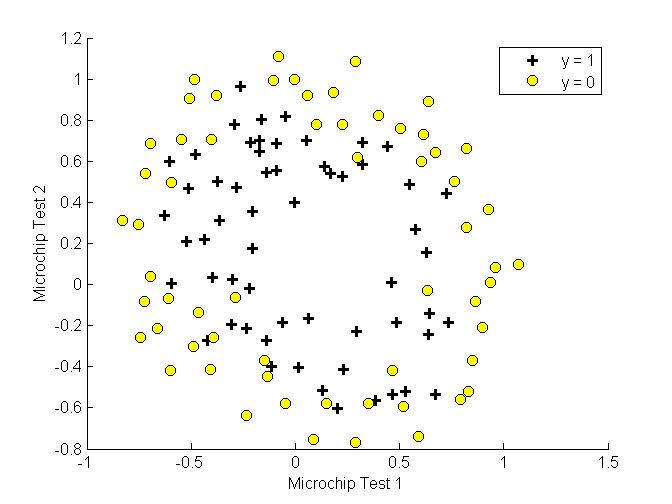
之后设置不同的$\lambda$,查看拟合效果