神经网络

当特征比较少时，可以使用线性回归或逻辑回归。但当特征很多时，例如图像像素非常多，传统的回归模型就不再适用了，需要使用神经网络。

• 
  上图就表示一个神经网络。$x_1$,$x_2$,$x_3$表示输入单元，$a_1$,$a_2$,$a_3$是中间单元，负责数据处理，并将处理后的结果传递到下次层。最后是输出单元，负责计算$h(x)$。
  $a_i^{(j)}$表示第$j$层的第$i$个激活单元。$\theta^{(j)}$表示从第$j$层映射到第$j+1$层时的权重矩阵;$\theta^{(j)}$行数为第$j+1$层的激活单元数量的行数，列数为第$j$层激活单元加一。
  下图是上面神经单元的计算过程。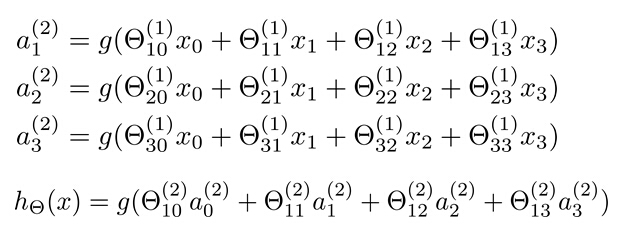
  
  使用向量会更加清晰，把$X$和$a$用矩阵表示：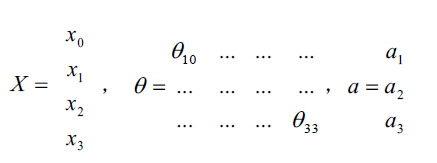
  
  令$z^{(2)}=\Theta^{(1)}x$，得到$a^{(2)}=g(z^{(2)})$，加上$a_0^{(2)}=1$，可以得到$z^{(3)}=\Theta^{(2)}a^{(2)}$,$h_{\Theta}(x)=a^{(3)}=g(z^{(3)})$

多种类别分类

当要分类的类别多于2个时，例如有4类时，最后输出层应该有4个神经元来表示4个分类，下面就是可能的一种情形：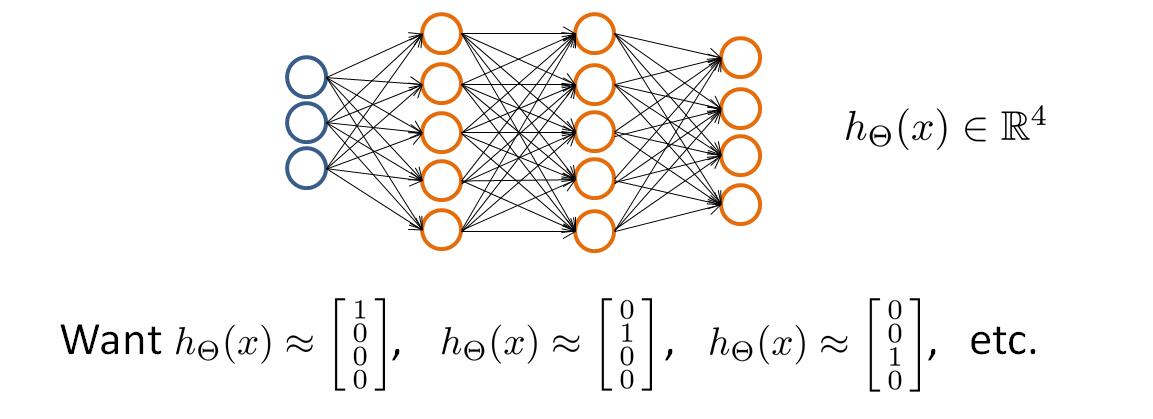

输出层的$h_\Theta(x)$中，只能有一个为1，其他为0。

损失函数

假设训练样本有$m$个，每个训练样本包含输入$X$和标签$y$，神经网络的层数为$L$，$S_l$表示每次神经元个数，
神经网络的损失函数为：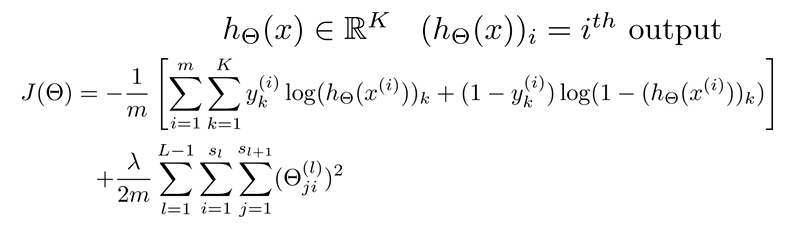

代价函数的本质是判断预测结果和真实结果的差距。神经网络中，会预测$K$个结果；可以使用循环，在预测中找出可能性最高的一个和真实值$y$进行比较。

归一化的项中，排出了$\theta_0$，对每一层的$\Theta$矩阵平方和。最里层的循环$j$表示循环所有行（有$s_l+1$层的激活单元数决定)；再往外一层循环$i$表示循环所有的列，有该层($s_l$层)的激活单元数所决定。

反向传播

神经网络有多层，为了计算偏导数，需要从后向前推导，即先计算最后一层的误差，在计算倒数第二层，以此类推，直到计算到第二层。以一个4层网络为例：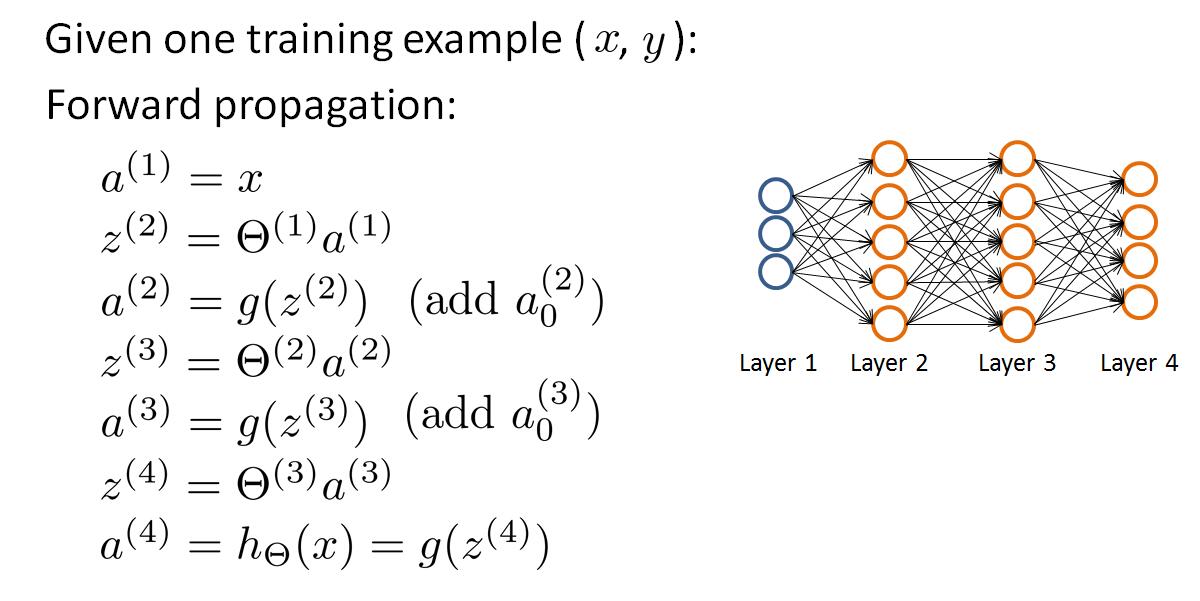

上面是正向传播的过程，反向误差传播如下：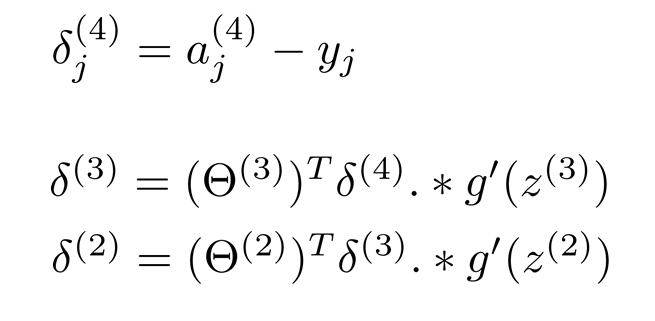

在不考虑归一化处理时：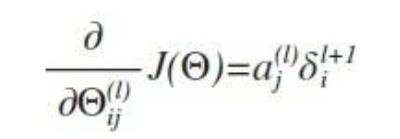

上面$l$表示当前所计算的是第$l$层，$j$表示当前计算层中激活单元的下标，即下一层第$j$个输入变量的下标；$i$表示下一层中误差单元的下标，是受到权重矩阵中第$i$行影响的下一层中的误差单元的下标。

如果输入是一个矩阵，考虑归一化处理。需要计算每一层的误差单元来计算代价函数的偏导数，误差单元矩阵中，用$\Delta{ij}^l$来表示第$l$层的第$i$个激活单元收到第$j$个参数的影响导致的误差。那么首先利用正向传播计算每一层激活单元，然后计算最后一层的误差，用这个误差反向计算各层误差，直到第二层。

求出所有$\Delta{ij}^l$之后，可以计算代价函数的偏导数了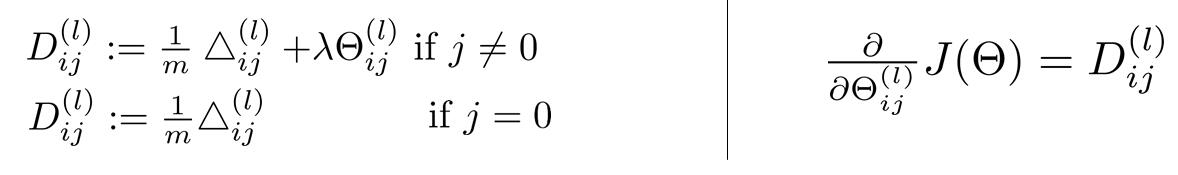

参考：Neural Networks: Representation