概述
上节讲到了图像分类以及kNN算法,kNN用作图像分类效果并不好。效果更好的分类算法是神经网络和卷积神经网络,它主要包括2部分
1、评分函数score function,把原数据映射为一个得分。
2、损失函数loss function,衡量预测得分和真实标签之间的差距。
最终的优化问题是最小化损失函数。
图像到标签得分的参数映射
首先定义图像像素数据到各个类别得分的映射。定义几个符号,训练集为$x_i \in R^D$,训练集的每个元素有个对应的标签$y_i$,$i=1 \dots N$,$y_i \in 1 \dots K$。即训练集有$N$个数据,维度为$D$,每个训练数据对应一个标签$y_i$,标签总共有$K$类。以CIFAR-10为例,$N=50,000, D=32 \times 32 \times 3 =3072, K=10$。定义评分函数$f: R^D \mapsto R^K$
线性分类器
一个常用的映射函数为
$$
f(x_i,W,b)=Wx_i+b
$$
$x_i$是图像数据,展开为一个列向量[D x 1]。矩阵$W$(维度[K x D])和向量$b$(维度[K x1])是函数的参数,分为被称为权重和偏置。
需要注意:
1、$Wx_i$得到的乘积是个列向量[K x 1],K个值对应K类。
2、优化的目的就是让上面函数的得分尽量和真实标签的值接近。
3、训练结束后,可以丢弃训练数据,只使用学到的参数值即可预测。
4、预测时只是矩阵的相乘和相加,速度很快。
解释线性分类器:
线性分类器是计算图像所有像素值的加权和,图像包括3个颜色通道。根据我们队权重(正/负)的设置,映射函数可以喜好或讨厌某一类颜色。例如,对于“船”这个类别,蓝色(海水)可能会在图像占比较大比例。这样在分类“船”时,蓝色对应的通道的可能会有比较多的正权重,而红色和绿色通道可能会有比较多的负权重。
下面是一个图像分的例子:
可以看出,更加倾向认为是一只狗。
类比高维空间
图像被展开为高维空间的列向量,可以把图像当做高维空间的一个点(例如CIFAR-10的中图像是3072维度空间的一个点)。线性分类函数就是来划分这个高维空间,假设这个高维空间是2维的,可视化后如下: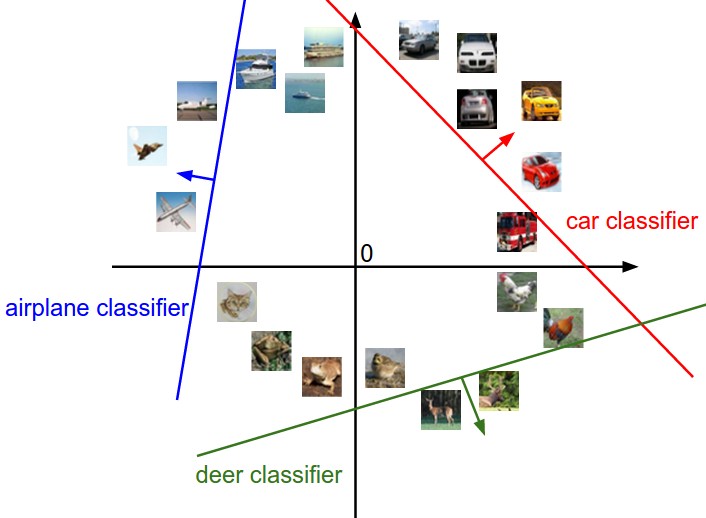
上图表示图像空间,每个点都是一个图像。矩阵$W$的每一行都是一条直线,控制其方向,$b$控制平移,直线上的点对应的得分为0,
线性分类器看做模板匹配
权重矩阵$W$的每一行可以看做匹配某一类的模板,每一类的打分就是图像和对应类别模板的乘积。下图是CIFAR-10训练后的模板的可视化图像:
可以看出“船”的模板包含很多蓝色的像素,这样会给蓝色通道像素分值比较高。
偏置技巧
可以把上面公式中,后面加的权重放到前面的矩阵乘法中,技巧就拓展矩阵多出一列,输入数据多出一维,最终公式变为:
$$
f(x_i,W)=Wx_i
$$
通过下图一看便知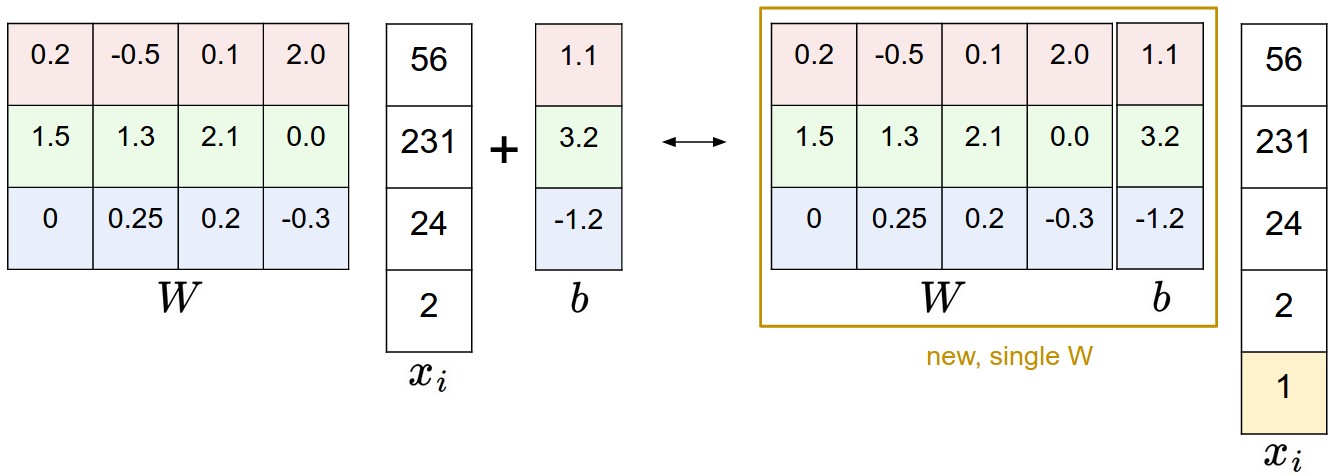
数据预处理
图像的像素范围是[0…255],但是在机器学习中经常要将特征归一化。经常用到的是把数据中心化center your data,通过减去每个特征的均值来做到的。例如减去像素的均值,可以是范围变为[-127…127]。有时还做进一步处理,使范围变为[-1,1]。0均值中心化非常重要,学了梯度下降就可以理解这一点了。
损失函数
前面通过评分函数来计算属于每一类的得分。这里通过损失函数来计算对得分的满意程度。损失函数又称作代价函数或目标。结果越好,损失函数值将越低,结果越差,损失函数的值将越高。
多类SVM loss
这里定义SVM的loss函数。SVM loss会使正确类别的得分比错误类别的得分至少高$\Delta$。用$s$代表分数,第i个图像对应第j类的得分$s_j=f(x_i,W)_j$,那么多类别SVM对于第i个图像的loss为
$$
L_i=\sum_{j \neq y_i}max(0, s_j-s_{y_i} + \Delta)
$$
一个例子
假设有3个类别,对应的得分$s=[13, -7, 11]$,真实类别是$y_i=0$,$\Delta=10$。损失函数有2项
$$
L_i = max(0, -7 - 13 + 10) + max(0, 11 - 13 + 10)
$$
上式中第一项为0,因为-7分值和真实得分相差20,大于$\Delta$;,第二项就不为0了,因为11分值和13只相差2,所以Loss函数就不为0了。
这一节是将线性分类器,所以Loss函数有以下形式
$$
L_i = \sum_{j\neq y_i} \max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta)
$$
下图就是多类别SVM loss可视化图。
上面损失函数有叫做hinge loss,形式为$max(0,-)$,有时会使square hinge loss(或L2-SVM)来代替,形式为$max(0,-)^2$。
正则化
上面提到的loss函数有bug。设想以下,假设假设评价函数能正确预测所有分类,且损失函数$L_i=0$;这样权重并不是唯一的。因为如果一组权重$W$符合这样的要求,那么$\lambda W$也符合这样的要求($\lambda >1$。如果得到评价函数的值不为0,那么评价函数的值也会放大$\lambda$倍。
可以通过对$W$加上些限制来移除上面的不确定性,得到一个唯一确定的权重系数矩阵。一般是通过正则化惩罚来实现$R(W)$来实现。最常用的惩罚是 $L2$ 范数:
$$
R(W)=\sum_k \sum_l W_{k,l}^2
$$
这个公式中不包含数据,是和数据无关的的loss。这样$L_i$就由2项组成了:data loss,regularization loss。
$$
L = \underbrace{ \frac{1}{N} \sum_i L_i }_\text{data loss} + \underbrace{ \lambda R(W) }_\text{regularization loss} \\
$$
展开后形式如下:
$$
L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)_j - f(x_i; W)_{y_i} + \Delta) \right] + \lambda \sum_k\sum_l W_{k,l}^2
$$
上式中$\lambda$是一个超参数,通过使用交叉验证来设置它。
引入正则化惩罚还可以带来其他许多性质,后面章节会提到。例如,在SVM中引入正则化后就有了最大间隔max margin这一性质,详细参考cs229。
正则化一个很好的性质是惩罚了大的权重值,这一可以提高模型泛化能力。限制权重大小后,没有那一维数据可能单独对评价函数带来很大影响。例如输入数据$x=[1,1,1,1,1]$,有两组权重$w_1=[1,0,0,0], w_2=[0.25,0.25,0.25,0.25]$,内积相等$w_1^Tx=w_2^Tx=1$。但是L2惩罚不同,对于$w_1$是1.0,而对于$w_2$是0.25,因此$w_2$优于$w_1$。直观上看,$w_2$更小,却值更加分散,这样输入数据的所有维度都会对评价函数有影响,而不是仅仅几个维度数据主要决定评价函数。因此,会有更好的泛化性能,减小过拟合。
需要注意,正则化只是针对权重$W$,而不针对偏差$b$,因为偏差对输入数据各个维度大小没有影响影响,它只是控制分类器的平移。
实践注意事项
设置$\Delta$:$\Delta$这个超参数一个常用的值是$\Delta = 1.0$。超参数$\Delta$和$\lambda$看上去是不同的超参数,实际上它们有同样的功能:平衡目标函数中的data loss和regularization loss。权重$W$的幅度直接影响评价函数的得分,例如放大权重幅度,得分也会变大,不同类别之间的得分差异也就变大了。$\Delta$是控制不同类别之间的得分差异,其他小可以通过放大或缩小权重幅度来控制。实际上权重的平衡是允许幅度有多大变化(通过$\lambda$来控制)。
和二项SVM关系:二项SVM是多项SVM的一个特例。
在原始形式中优化:如果以前学过SVMs,可能会听过核方法、对偶、SMO算法等。在神经网络中,往往使用目标函数的原始形式。许多模板函数在技术上不可分,但是实际中可以使用次梯度。
其他形式的SVM:本节的多类SVM只是一种,还有其他形式。
Softmax分类器
除了SVM分类器外,还有一种常用的叫做Softmax分类器,它是二元逻辑回归泛化到多元的情况。Softmax分类器的输出不是得分,而是对应类别的概率。Softmax分类器中,映射函数$f(x_i; W) = W x_i$并没改变,把得分当做未归一化的对数概率,把hinge loss替换为交叉熵 loss:
$$
L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text{or equivalently} \hspace{0.5in} L_i = -f_{y_i} + \log\sum_j e^{f_j}
$$
其中,$f_j$表示第j类的得分。整个数据集的loss是$L_i$加上正则化项$R(W)$。函数$f_j(z) = \frac{e^{z_j}}{\sum_k e^{z_k}}$叫做softmax函数,它把得分向量转换为概率向量。
信息论角度:一个真实分布$p$和气估计分布$q$的交叉熵定义如下:
$$
H(p,q)=-\sum_xp(x) \log q(x)
$$
Softmax分类器是最小化估计的分布($q = e^{f_{y_i}} / \sum_j e^{f_j}$)和真实分布($p=[0,…,1,…,0]$,只有第$yi$个为1)之间交叉熵。交叉熵可以看做熵和相对熵的和相对熵的和**$H(p,q) = H(p) + D{KL}(p||q)$,真实分布$p$**的熵是零,所以最小化交叉熵等价于最小化相对熵。
概率解释:公式
$$
P(y_i \mid x_i; W) = \frac{e^{f_{y_i}}}{\sum_j e^{f_j} }
$$
已知输入数据$x_i$和权重参数$W$,上式可以看做对应类别$y_i$的归一化概率。评价函数的输出向量没有归一化,直接当做对数概率的输入,之后用对数概率除以所有概率的和来进行归一化,这样概率的和为1。从概率论角度看,我们再最小化正确分类的负概率(即最大化正确分类的概率),这是最大似然估计(Maximum Likelihood Estimation)。这样损失函数中的正则化部分$R(W)$可以看过权重矩阵$W$的高斯先验,这样最大似然估计变成了最大后验概率估计(Maximum a posteriori)。
实践问题:数值稳定:当写代码实现Softmax函数时,会涉及到$e^{f_{y_i}}$和$\sum_j e^{f_j}$,因为指数的原因,这些数值可能会非常大。除以很大的数值可能会引起数值不稳定,可以使用归一化的技巧。在分子和分母同时乘以一个常数,分数的数值不变:
$$
\frac{e^{f_{y_i}}}{\sum_j e^{f_j}}
= \frac{Ce^{f_{y_i}}}{C\sum_j e^{f_j}}
= \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}}
$$
$C$通常设为$\log C = -\max x_if_j$,这样分数向量中最大的值为0。
SVM vs. Softmax
下面图像可以帮助对比两者区别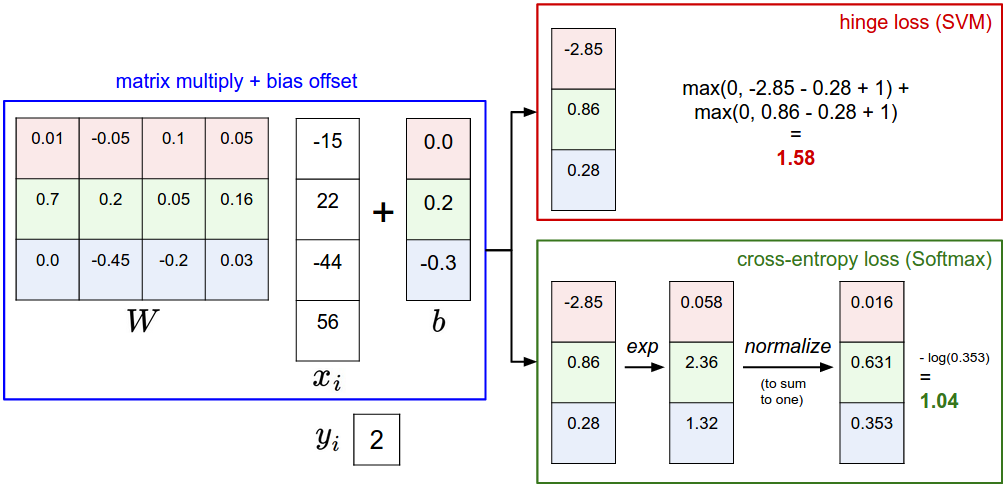
Softmax分类器计算每类的概率:SVM计算每类的得分,这样不易直接解释。Softmax计算每类的概率。超参数$\lambda$控制概率的集中或离散程度。
实践中,SVM和Softmax常常是相似的:SVM和Softmax性能差别不大,不同的人对哪种效果更好持不同的观点。和Softmax相比,SVM更加局部化(local objective),它只关心小于间隔$\Delta$的部分,例如$\Delta = 1$,那么分值[10, -100, -100]和[10, 9, 9]对于SVM来说,其loss函数值相同;但是对于softmax就不同了。Softmax的loss函数只有在完全正确情况下才会为0。
总结
1、定义了评价函数,线性函数的评价函数依赖权重$W$和偏置$b$。
2、和kNN使用不一样,参数化方法训练时间比较久,预测只是矩阵相乘。
3、通过一个trick,可以把偏置加入到矩阵相乘中。
4、定义了loss 函数,介绍了常用的SVM和Softmax loss。对比了两者的区别。
如果求解最优的参数,这设计到优化,是下一节讲解的问题。