介绍

上节介绍了图像分类中两个重要的组成部分：
1、评价函数score function
2、损失函数loss function

线性函数$f(x_i, W) = Wx$，那么SVM的loss为:
$$ L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)_j - f(x_i; W)_{y_i} + 1) \right] + \alpha R(W) $$
现在介绍第三个重要组成部分：优化optimization。优化的过程是寻找参数$W$，是的loss函数的值最小。

铺垫：一旦我们理解了这三个核心组成部分如果相互作用，我们将会重新再回顾评价函数，把它扩展比线性映射更复杂的形式。首先扩展到神经网络，之后神经网络。损失函数和优化不变。

可视化loss函数

loss函数一般都是高维的，难以可视化。但是，我们可以在高维空间切一条线或一个平面来获取一些直观的理解。例如，生成一个矩阵$W$，它代表高维空间的一个点。我们可以随机生成一个方向$W_!$，沿着这个方向，用不同的$\alpha$来计算$L(W+\alpha W_1)$的值，这时$\alpha$可以当做x轴，而loss function可以当做y轴。也可以生成两个方向，根据$a,b$变化计算$L(W+a W_1 + b W_2)$的值，这时$a,b$可以分别代表x轴和y轴，loss函数的值可以用颜色来区分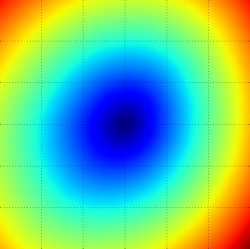

上图中是SVM的loss，最左边是一维空间。右边两个是2为空间，蓝色代表低值，红色代表高值。

可以看出svm的loss函数是分段的，SVM的loss函数为：
$$ L_i = \sum_{j\neq y_i} \left[ \max(0, w_j^Tx_i - w_{y_i}^Tx_i + 1) \right] $$
SVM的loss只对小于$\Delta$部分的差值起作用，对于大于$\Delta$的部分，它为零。因此是分段的。

SVM的loss虽然是分段的，但是它是凸函数。优化这类问题，可以参考斯坦福的凸优化。
如果把评分函数拓展到神经网络，loss函数就不是凸函数了

不可导函数。因为max算子，函数存在不可导的点。但是次梯度subgradient，本节接下来将交叉使用次梯度和梯度。

优化

loss函数可以衡量权重$W$的好坏。优化的目的就是找到一个$W$是的loss函数最小化。本节优化是以svm的loss函数为例，它是凸函数；但是我们最终的目的是优化神经网络，不能简单使用由凸优化得到的方法。

随机搜索

因为可以很简单的检验参数$W$的好坏。最简单的想法是随机找一些参数，记录它们的loss，找到最好的。
使用随机搜索，得到的准确率为15.5%，比10%高一点。

随机本地搜索

你可能想到的是随机找一个方向，如果这个方向可以减小loss，那么久向这个方向前进一步，更新权重。
使用这个策略，在测试集上的准确率为21.4%，比第一个策略好一点，但是还是浪费计算资源。

沿着梯度

在随机本地搜索中，目的是在梯度空间找到一个方向，使得loss函数值减少。事实上，不用随机找这个方向；可以计算出loss函数下降最快的方向。这个方向就是梯度的负方向。

在一维空间，梯度就是函数在某一点瞬时变化率。在多维空间，输入变量是向量，梯度就是在各个变量方向的瞬时变化率组成的向量（梯度也叫作导数）。一维空间计算导数公式如下：
$$ \frac{df(x)}{dx} = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} $$
当函数输入不是一个数值，而是一个向量是，我们把导数叫做偏导（partial derivatives），梯度就是各个维度上的偏导组成的向量。

计算梯度

有两种方法计算梯度：一种缓慢逼近的方法是数值梯度（numerical gradient），另一种更快速准确但是容易出错，需要使用微积分，是分析梯度（analytic gradient）

数值梯度

使用数值，逼近计算梯度，有两个公式：
$$ \frac{df(x)}{dx} = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} $$
还有一种形式是中心差公式（centered difference formula），它效果更好
$$ \frac{df(x)}{dx} = \lim_{h \to 0} \frac{f(x+h) - f(x - h)}{2h} $$
详细内容，可以参考wiki。

计算梯度，应该让$h$尽可能小，一般使它在$1e^{-5}$级别。

更新权重时，要注意，是使用梯度的负方向，因为梯度是函数增长最快的方向，其负方向才是下降最快的方向。

梯度只是告诉了我们方向，但是没告诉我们一步走远，这个参数是步长（也叫作学习率），它也是一个超参数。

效率问题：计算梯度时，需要计算每一个参数的梯度。在神经网络中，参数量巨大，计算每一个参数的梯度，也给我们带来了效率问题。可以找到更好的方法。

分析梯度

数值梯度求到的是近似梯度，因为$h$不能等于零。分析梯度需要使用微积分，它是计算得到真正的梯度，而且它非常快。但是分析梯度容易出错；这也是为什么在实践中，经常使用分析梯度和数值梯度对比来验证分析梯度。这叫做梯度检验gradien check。

以SVM的loss为例，求某个点上的梯度:
$$ L_i = \sum_{j\neq y_i} \left[ \max(0, w_j^Tx_i - w_{y_i}^Tx_i + \Delta) \right] $$
对权重$w{yi}$求导
$$ \nabla_{w_{y_i}} L_i = - \left( \sum_{j\neq y_i} \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) \right) x_i $$
上式中，$\mathbb{1()}$是指示函数，如果后面括号条件为true，那么值为1，否则值为零。需要注意一点，计算梯度，只需要计算分类错误对应权重$W$那些行的梯度，正确分类的不用计算。例如正确标签为$s{yj}$，那么梯度是：
$$ \nabla_{w_j} L_i = \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) x_i $$

梯度下降

计算好梯度后，就可以用梯度更新权重参数，这叫做梯度下降。

最简单的使用梯度下降的方法就是用一个循环，在循环中不计算梯度，更新权重。这是最基本的思想。但还有其他使用梯度下降的方法。

Mini-batch梯度下降

当训练集比较大时，以计算机所有样本来计算梯度，之后更新一次参数。这样做有点浪费。一个常用的方法是使用训练集一批样本来计算梯度。这个方法之所以也管用，是因为训练集样本是相关的。一小批样本可以看做训练集的近似。

随机梯度下面Stochastic Gradient Descent (SGD)

Mini-bach梯度下降中，当每批样本只包含一个样本是，就是随机梯度下降了。随机梯度下降在线梯度下降算法；在实际应用中比较少见随机梯度下降，因为一次计算多个样本梯度更加高效。

技术上SGD是指用一个样本来计算梯度，实际中经常听到SGD实际指mini-bach（MGD指Minibatch Gradient Descent, 或者BGD指Batch Gradient descent，它们并不常见）。Mini-batch的大小也是一个超参数，但是它不需要使用交叉验证来获取；实际经常根据内存大小来制定，常常使用2的幂：32、64、128，这样更容易实现向量化操作，且运算更快。

总结

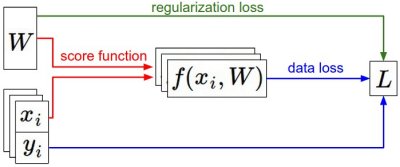
数据集$(x,y)$已知且固定。权重以一个随机数开始。前向传播由评价函数计算得分。loss函数包含两部分：data loss是计算评分和真实值的loss；正则化loss只和权重有关。在梯度下降过程中，计算梯度，更新参数。

在这一节中：
1、loss函数类似高纬度的地形优化，我们要到达最底部。SVM的loss是分段的。
2、使用迭代增强方法优化loss函数。
3、梯度给出了loss函数下降最快的方向。
4、梯度下降过程中，要使用一个超参数：步长（学习率）。学习率的设置需要技巧。
5、数值梯度和分析梯度。两者优缺点，前者可以检验后者。
6、介绍了梯度下降算法。