介绍
这节介绍反向传播的直观理解。使用链式法则递归求导
函数$f(x)$,其中$x$是输入变量,我们需要计算$x$的导数$\nabla f(x)$。这个函数$f(x)$可以是loss函数,计算loss函数关于权重和偏置$W,b$的导数,依次更新它们。
简单表达式和解释梯度
函数有两个变量$f(x,y)=xy$,可以得到
$$
f(x,y) = x y \hspace{0.5in} \rightarrow \hspace{0.5in} \frac{\partial f}{\partial x} = y \hspace{0.5in} \frac{\partial f}{\partial y} = x
$$
一个变量的导数,表示它的值变化时对整个表示式影响的大小。
$\nabla f$表示偏导数向量,$\nabla f = [\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}] = [y, x]$
对加法求导:
$$
f(x,y) = x + y \hspace{0.5in} \rightarrow \hspace{0.5in} \frac{\partial f}{\partial x} = 1 \hspace{0.5in} \frac{\partial f}{\partial y} = 1
$$
对max算子求导
$$
f(x,y) = \max(x, y) \hspace{0.5in} \rightarrow \hspace{0.5in} \frac{\partial f}{\partial x} = \mathbb{1}(x >= y) \hspace{0.5in} \frac{\partial f}{\partial y} = \mathbb{1}(y >= x)
$$
上面变量大的值才对表达式有影响,变量小的值,导数为零。
使用链式法则计算复合表达式
以一个稍微复杂一点的计算为例$f(x,y,z) = (x + y)z$,可以把这个函数分为2个$q = x + y$,$f = qz$。先对$q,z$求导得到$\frac{\partial f}{\partial q} = z, \frac{\partial f}{\partial z} = q$,在用$q$对$x,y$求导$\frac{\partial q}{\partial x} = 1, \frac{\partial q}{\partial y} = 1$,根据链式法则$\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial x}$
上面求解过程,可以用下图表示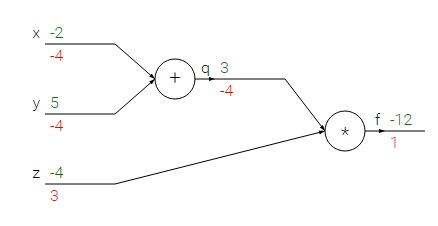
上图中,绿色表示前向传播,红色表示反向传播。
反向传播直观理解
反向传播是局部处理过程。每个神经单元在得到输入后,可以立即计算两件事1、输出,2、关于输入的局部梯度。神经单元不需要知道整个网络的结构就可以完成这两件事。前向传播完成后,在反向传播时,只需要对路径上的局部梯度相乘就可以得到最终输出对于某个变量的梯度值。
##模块化:Sigmoid例子
任何函数都可以看做一个神经元,可以把多个神经元组成一个,或把一个函数拆分为几个门单元。看下面的表达式
$$
f(w,x) = \frac{1}{1+e^{-(w_0x_0 + w_1x_1 + w_2)}}
$$
这个函数有多个计算组成,除了上面介绍的加、乘、max,还有四种:
$$
f(x) = \frac{1}{x}
\hspace{1in} \rightarrow \hspace{1in}
\frac{df}{dx} = -1/x^2
\\\\
f_c(x) = c + x
\hspace{1in} \rightarrow \hspace{1in}
\frac{df}{dx} = 1
\\\\
f(x) = e^x
\hspace{1in} \rightarrow \hspace{1in}
\frac{df}{dx} = e^x
\\\\
f_a(x) = ax
\hspace{1in} \rightarrow \hspace{1in}
\frac{df}{dx} = a
$$
上面的计算过程可以用下图表示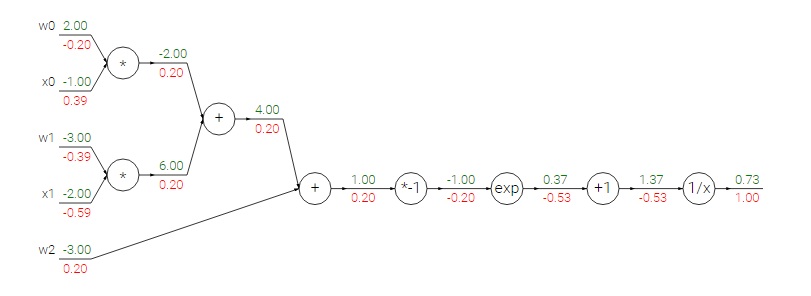
其中$w = [2,-3,-3],x = [-1, -2]$
sigmoid函数是常用的激活函数,对它的求导,计算如下
$$
\sigma(x) = \frac{1}{1+e^{-x}} \\\\
\rightarrow \hspace{0.3in} \frac{d\sigma(x)}{dx} = \frac{e^{-x}}{(1+e^{-x})^2} = \left( \frac{1 + e^{-x} - 1}{1 + e^{-x}} \right) \left( \frac{1}{1+e^{-x}} \right)
= \left( 1 - \sigma(x) \right) \sigma(x)
$$
实现提示:分段反向传播。把前向传播分段进行,方便计算导数和反向传播。
反向传播实践:分段计算
有如下函数
$$
f(x,y) = \frac{x + \sigma(y)}{\sigma(x) + (x+y)^2}
$$
先写代码实现forward1
2
3
4
5
6
7
8
9
10
11
12x = 3 # example values
y = -4
# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # sigmoid in numerator #(1)
num = x + sigy # numerator #(2)
sigx = 1.0 / (1 + math.exp(-x)) # sigmoid in denominator #(3)
xpy = x + y #(4)
xpysqr = xpy**2 #(5)
den = sigx + xpysqr # denominator #(6)
invden = 1.0 / den #(7)
f = num * invden # done! #(8)
在实现时,创建了一些中间变量sigy, num, sigx, xpy, xpysqr, den, invden,这些都是简单的表达式。在反向传播时,在这些变量前面加上d表示梯度
1 | # backprop f = num * invden |
注意:
1、对前向传播过程中的变量进行缓存,因为在反向传播时也会用到。
2、如果$x,y$在前向传播时,使用了多次;那么在反向传播时要使用+=来代替=。我们要累积梯度,使用=会覆盖掉前面计算好的梯度。
方向传播流的模式
反向传播中的梯度可以直观的解释一下。神经网络中最常用的三个门单元为$add,mul,max$,可以直观的看一下它们三个在反向传播中,对梯度的影响。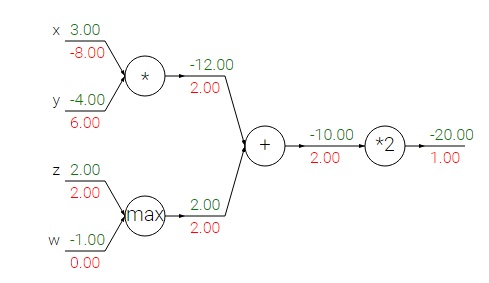
add:加法是把梯度不变的分到下一个门单元。
max:max算子是把梯度分到值比较大的一个单元。
mul:乘法是把梯度乘以一个值传到下一个门单元。$f=xy$,那么传到$x$的梯度要乘以$y$,同理$y$的梯度。
注意,权重和数据的乘积$w^Tx_i$,如果有某个权重很大,那么某个维度的输入数据梯度会很大,这样这个维度的数据对结果有很大影响。因此要正则化权重,限制梯度幅度。
向量化梯度操作
上面的例子都是单个变量的,神经网络中的运算都是以矩阵或向量为单位的。求梯度以及梯度反向传播,都可以用矩阵或向量乘法。1
2
3
4
5
6
7
8
9# forward pass
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)
# now suppose we had the gradient on D from above in the circuit
dD = np.random.randn(*D.shape) # same shape as D
dW = dD.dot(X.T) #.T gives the transpose of the matrix
dX = W.T.dot(dD)
注意,在分析梯度是,不用记住它的表达式,因为可以通过维度推导出来。dW维度和W维度大小一样,它等于dD和X的乘积。
总结
1、对梯度有了直观理解,知道梯度如何在网络中传播,如何影响输出。
2、对梯度计算时,使用分段计算。把函数分为更小的模块,可以更好地计算梯度,使用链式法则得到最终梯度。