2016-09-06

cs231n-(5)神经网络-1：建立架构

介绍激活函数，建立神经网络

简单介绍

在介绍线性分类器是，介绍了评分函数$s=Wx$，例如分类CIFAR-10时，$x$是$[3072 \times 1]$的向量，$W$是$[10 \times 3072]$的矩阵，输出是10个类别的得分。

上面的计算时线性的；而神经网络往往是非线性的。例如一个神经网络$s = W_2 \max(0, W_1 x)$。这里$W_1$是$[100 \times 3072$的矩阵，把图像转换为一个向量；函数$max(0,-)$是非线性运算，非线性运算有很多种。$W_2$是$[10 \times 100]$的矩阵，这样就能得到10个评分了。非线性运算至关重要，如果没有非线性运算，这两步运算得到的结果和输入也是线性关系。权重参数$W_1,W_2$可以通过随机梯度下降求得，梯度可以通过链式求导法则计算。

单个神经元模型

神经网络是由生物学上的神经元激发而创建；在机器学习领域的工程实践上表现优异。

生物学动机和连接

大脑的的基本组成单位是神经元。在人的神经系统中，大概有860亿个神经元通过$10^{14} \sim 10^{15}$个突出连接。下图左边是一个神经元，右边是模仿神经元的数学模型。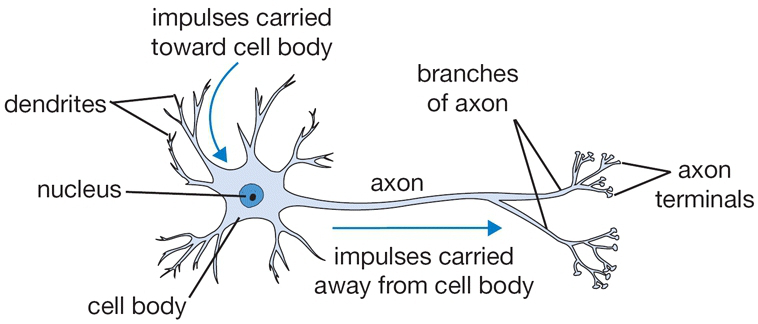

神经元从突出接收到信号，在神经元信号和权重相乘，随后再相加，然后经过一个非线性函数输出。这个非线性函数叫做激活函数。

上面建立的模型只是一个粗糙简单的模型，真实情况远比上面负责，具体可以参考这里和这里

单个神经元当做线性分类器

上面建立的模型和线性匪类器很像。把loss函数应用到神经元的输出就可以看做是线性分类器了。

二元分类器：把函数$\sigma(\sum_iw_ix_i + b)$当做分类的概率。
二元SVM分类器：在输出后面加上一个hinge loss函数，可以训练成一个二元SVM分类器。
正则化解释：正则化函数让$W$趋向于零，这里可以理解为逐渐忘记。

常用的激活函数

激活函数的输入都是一个数字，然后进行非线性运算。下图是几个激活函数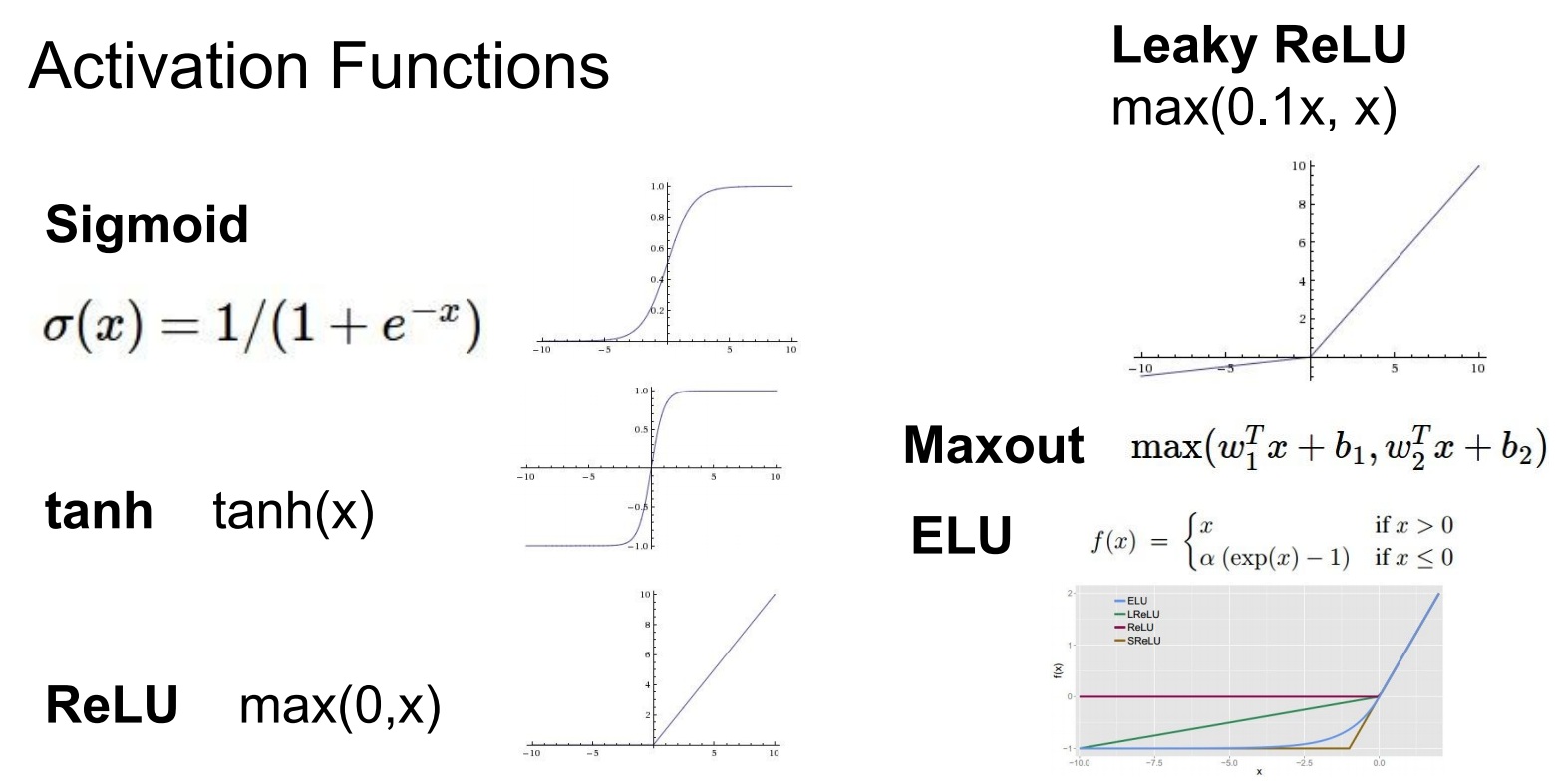

Sigmoid

$$ \sigma(x) = 1 / (1 + e^{-x}) $$

它把输入压缩到(0,1)之间；非常大的负数趋向于0，非常大的正负趋向于1。Sigmod现在已经少用了，因为
1、Sigmoid有梯度消失的问题。
2、Sigmoid输出不是零中心的。例如输出全是正数，那么下一层输入就全是正数，这将导致梯度要么全是正数，要么全是负数；在使用梯度下降算法时，呈现出Z字下降。这个问题可以通过批量梯度下降解决。

Tanh

$$ \tanh(x) = 2 \sigma(2x) -1 $$

它的输出是零中心的[-1,1]，但是它同样存在梯度消失问题。

ReLU

$$ f(x)= \max(0,x) $$

ReLU近几年比较受欢迎。它有以下优缺点
1、优点：使用SGD时，它比Sigmoid/Tanh收敛速度快。
2、优点：和Sigmoid和Tanh相比，它计算简单。
3、缺点：脆弱，容易死掉。死掉是指，比较大的梯度经过神经元后，可以导致ReLU输出都小于0，即不再激活。这个可以同构调整学习率部分解决。

Leaky ReLU

$$ f(x) = \mathbb{1}(x < 0) (\alpha x) + \mathbb{1}(x>=0) (x) $$

即

$$
f(x) = \max(\alpha x, x)
$$

其中$\alpha$是一个很小的常数。$Leaky ReLU是解决ReLU死掉问题的。详细介绍参考这里

Maxout

归纳ReLU和Leaky ReLU，得到更通用的一般形式
$$ \max(w_1^Tx+b_1, w_2^Tx + b_2) $$
例如，当$W_1=0,b_1=0$时就是ReLU函数。它克服了ReLU的缺点，保留了其优点。但是其参数增加了一倍。

在神经网络中，很少见到在同一个网络的不同神经元中使用不同的激活函数，即使这样做没有什么问题。

神经网络结构

神经网络是由神经元组成的无环图；一个神经元的输出可以作为另一个神经元的输入，但是神经网络中不存在环路（这样会造成前向传播死循环）。神经网络是分层的，最常见的层是全连接层。在全连接层中，神经网元与前一层和后一层的每个神经元都相连。下图就是由全连接层组成的两个神经网络。

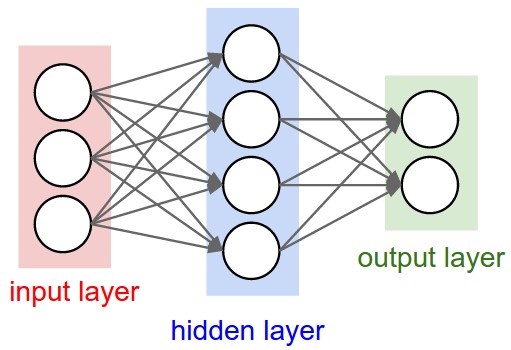
命名规则：在定义神经网络层数时，不包括输入层。例如上图中，左边的神经网络有2层，右边的神经网络有3层。
输出层：输出层通常没有激活函数，因为输出层一般用来评分，它的值范围是任意的。
定义神经网络大小：最常用的有神经元个数和参数个数。
例如，上图左边升级网络有6个神经元；有[3x4]+[4x2]=20个权重和4+2=6个偏置。右边升级网络有9个神经元，有[3x4]+[4x4]+[4x1]=32个权重和4+4+1=9个偏置。

前向传播计算例子

神经元按层来组织的一个原因是因为这样的结构，使用矩阵向量运算特别方便。以上图右边神经网络为例。输入是[3x1]向量。一个层的所有连接可以用一个矩阵表示，第一个隐藏层权重$W_1$大小为[4x3]，偏置$b_1$为[4x1]；每个神经元的权重时$W_1$的一行，这样权重和输入乘积（矩形乘以向量）加上偏置（向量）就是激活函数的输入。同理，可以得到$W_2$为[4x4]$的矩阵，$W_3$是[1x4]的向量。
用代码表示

# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)

其中W1,W2,W3,b1,b2,b3是要学的参数。

表述能力

可以把带全连接的神经网络看做一个函数，这个函数的参数是网络中的权重。怎么衡量这个函数的表述能力呢？是否存在神经网络不能表达的函数。

可以证明，包含至少一个隐藏层的神经网络可以近似任何函数。证明参考 Approximation by Superpositions of Sigmoidal Function和intuitive explanation。

既然2层神经网络可以近似任何函数，那么为什么还要更深的网络？因为在实际中，2网络相对较差。实际中用更深的网络，因为它们更加平滑、更好的符合统计特性，可以通过梯度下降等算法学习。

3层的神经网络比2层神经网络效果好，但是更深的网络（4,5,6）层网络未必更好；这时神经网络情况。但是在卷积神经网络中，情况就不同了，更深的网络往往表现更好。

更多内容，参考：
Deep Learning book in press by Bengio, Goodfellow, Courville, in practicularChapter 6.4.
Do Deep Nets Really Need to be Deep?
FitNets: Hints for Thin Deep Nets

设置层的个数和大小

在使用神经网络时，该不该用隐藏层？如果用，用多少个隐藏层？每层设置多大？
随着网络层数增加，网络的表达能力也会增加。以一个二元分类为例，下面是不同隐藏层的效果

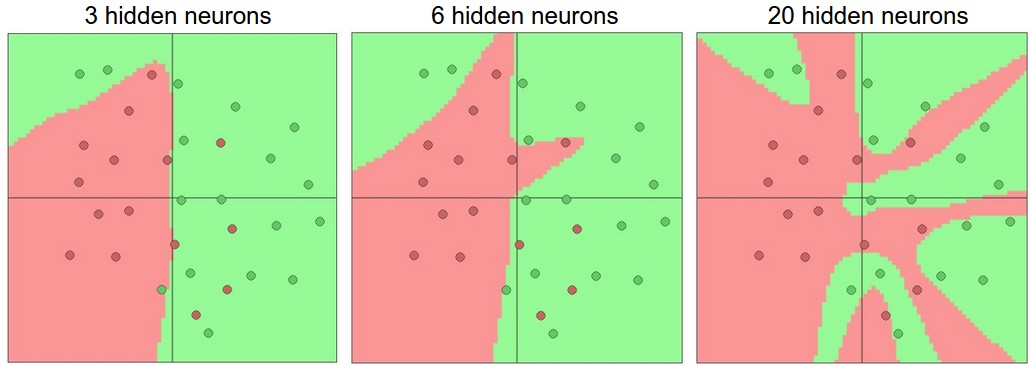
一个动态的例子在这里
可以看到，更深的网络拟合的效果更好。但是拟合训练集更好时，可能存在过拟合问题；我们想要的模型应该有比较好的泛化能力。

限制过拟合的方法很多，例如L2正则化，dropout，输入噪声等。实际中，往往使用这些方法来限制过拟合比减少神经元数目效果更好。下图就是L2正则化上面对应网络的图片：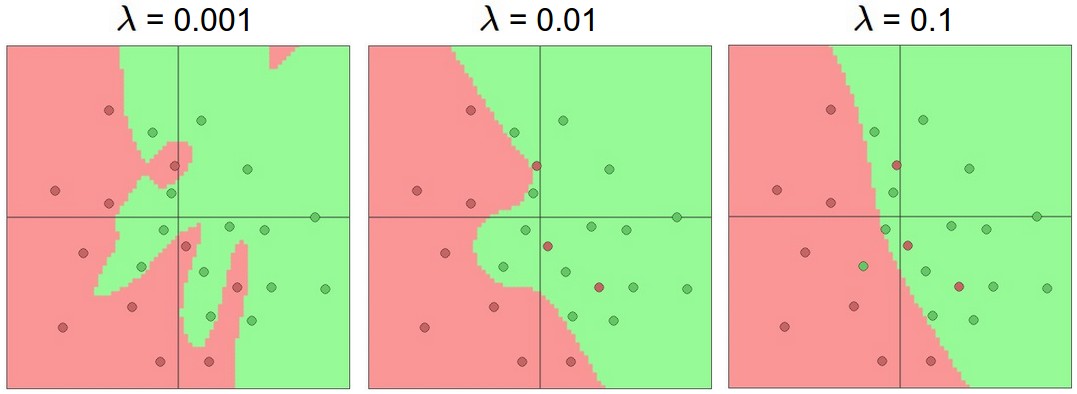

不要通过减少神经元来防止过拟合的另外一个原因是因为，小的神经网络更难训练。虽然小的神经网络拥有更少的局部极小值，且很容易收敛到局部极小值，但是实际中这些极小值效果很差，它们的loss很大。更深的网络显然有更多的局部极小值，但是这些极小值表现效果更好。神经网络是非凸优化问题，数学上很难表述。可以参考The Loss Surfaces of Multilayer Networks

总结

1、介绍了几个激活函数。
2、介绍了神经网络和全连接层。
3、神经网络可以近似所有函数。
4、大的神经网络往往效果更好，但是需要其他手段防止过拟合。

KangBing