cs231n-(5)神经网络-2：设置数据和Loss

cs231n笔记

数据预处理，权重如何初始化，正则化方法，损失函数

数据预处理

神经网络输入的数据往往要经过预处理。假设数据X大小为[N x D]，其中N表示元素个数，D表示维度。

减去均值

最长用的就是减去每个特征的均值（均值常常有训练集计算得到），减去均值的几何意义是将数据中心大致移到零点。。使用python时，可以用X-=np.mean(X, axis = 0)算得均值。如果是图像，常常减去RGB通道的均值。

正则化

正则化是指将数据各个维度归一化，即变化范围相同。一般有两种方法：1、将数据均值设为零（如减去均值），之后除以标准差：X /= np.std(X, axis=0)。2、不同维度的数据范围相差很大，且重要性相同，将其最大值和最小值分别变换为+1和-1。

下去就是原始数据，零中心化，正则化处理的效果。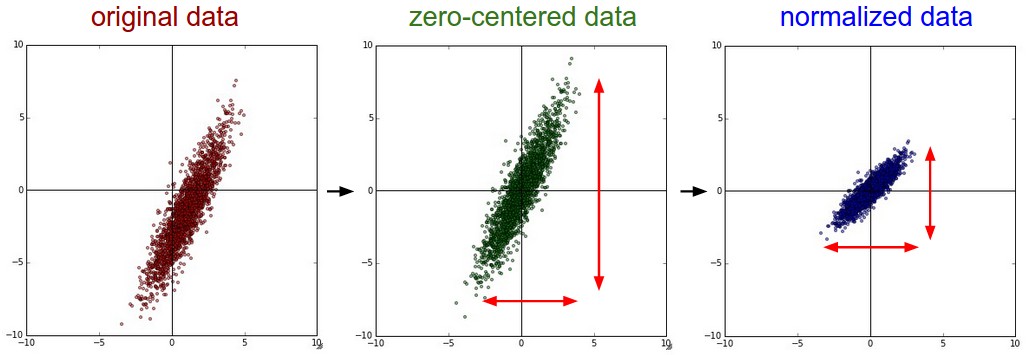
cs231n6_01.jpeg

PCA and Whitening

PCA是用来降维，假设已经完成了零中心化和归一化，降维过程如下：
先计算协方差矩阵

1
2
3
# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix

协方差矩阵中(i,j)位的数据表示i维度和j维度数据的协方差；对角线上数据表示某一维度的方差。协方差矩阵是对称的半正定矩阵，对它进行SVD分解：

1
U,S,V = np.linalg.svd(cov)

得到U是特征向量矩阵，它的每一列都是一个特征向量，S是特征值向量，因为协方差矩阵是对称的半正定矩阵，所以它等于特征值平方。为了去除相关性，将已经中心化的数据映射到特征向量上

1
Xrot = np.dot(X, U) # decorrelate the data

其中U的每一列都是标准正交特征向量，且已经按照特征值由大到小排列（np.linalg.svg返回时已经排列）。与特征向量相乘，相当于对X的数据做一个旋转映射，映射到特征向量对应的正交基上。可以只保留前面较大特征值对应的特征向量，丢弃较小值对应的特征向量，以此来降维。这种方法叫做Principal component analysis

1
Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]

通过这个操作，保留了前100维度数据（以方差大小为标准）。

经过PCA处理的数据，可以再经过白化Whitening处理。白化是指PCA处理后的数据，每个维度除以其特征值。几何解释就是服从多维度高斯分布的数据，经过白化处理后，服从均值为零，协方差相等的分布。

1
2
3
# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

上面处理为白化操作，分母加上1e-5为防止分母为零。这样的操作把所有维度数据拉伸到相同范围，可能会放大噪声，实际中可以通过增大分母（加上比1e-5更大的值）来平滑。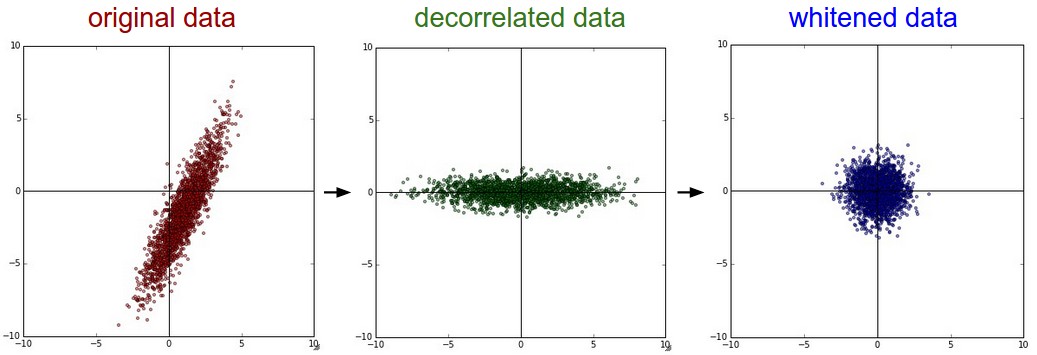
cs231n6_02.jpeg

上图左边分布为原始数据。中间为PAC处理后的数据，可以看出PCA处理后，将坐标轴旋转，可以看出横轴信息量大，如果只保留一维数据，要丢弃纵轴数据。右边为白化处理后的数据，数据范围相同了

使用CIFAR-10来展示PCA和白化
cs231n6_03.jpeg
上图中，最左边为原始数据，每张图片可以看做是3072的列向量。第二张为特征向量中，前144个（按照特征值排列）。第三张为经过PAC降维处理后，只保留144维特征的图片；图片变模糊了，说明只保留了低频部分。最后一张为白化后的图片。

注意：CNN不需要进行PCA和白化操作，这里提到只是讲解数据处理的一般方法。
数据预处理，只能在训练集上应用。应该先将数据分为训练集、验证集、测试集，之后在训练集上应用数据预处理。

权重初始化

训练神经网络前，要先初始化权重。

全部初始化为零

权重最终的值我们不知道，但是根据前面数据预处理过程，大概可以猜到，权重最终应该是一般为正，一般为负。但是权重不能全部初始化为零。如果全部初始化为零，那么所有神经元输出将相同，计算得到所有梯度都相同，权重更新相同，最终得到的权重也相同。

小的随机数

因为正则化，权重要比较小，但是又不能对称；那么可以用小的随机数来初始化。这样计算得到不同梯度，迭代更新权重会趋向不同。例如这样初始化。W = 0.01 * np.random.randn(D, H)，randn是生成零均值单位方差的高斯分布。这样初始化，每个神经权重向量是从高维高斯分布随机采样而来；也可是使用随机生成的随机数。但是在实际中，这样初始化效果不好。

小的权重并不一定会得到好的效果。神经网络中，如果权重比较小，那么反向传播时，梯度就比较小。这样会减小梯度传播的信号，在深度神经网络中也是个问题。

校准方差

如果神经元输出有着相似的分布，那么收敛速度回加快。前面提到的权重初始化方法，随着输入增大，输出的方差会增大。通过除以sqrt(n)，其中n是输入个数，可以将输出方差归一化到1；例如这样初始化w = np.random.randn(n) / sqrt(n)。

不考虑非线性激活函数，假设输出$s = \sum_i^n w_i x_i$，那么计算输出方差和输入关系如下：

$$ % $$

上面第三步中，用到了假设$E[x_i] = E[w_i] = 0$（注意，有些并不等于零，例如ReLU），最后一步假设了$x,w$服从相同分布。如果想要输出和$x$有相同的方差，那么$n \text{Var}(w)$必须为1，所以得到上面初始化方式w = np.random.randn(n) / sqrt(n)。

论文Understanding the difficulty of training deep feedforward neural networks推荐初始化方式为$\text{Var}(w) = 2/(n_{in} + n_{out})$，其中$n{in} ,n{out}$分布表示前一层和后一层网络中单元个数。论文 Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification 提出，针对ReLU初始化，网络中神经元方差为$2.0/n$，这样初始化变为w = np.random.randn(n) * sqrt(2.0/n)；在实践中使用ReLU时，推荐这样初始化。。

稀疏初始化

首先将所有权重初始化为零，但是为了避免对称，随机在层之间连接个别神经全，权重初始化可以使用小的高斯分布，连接个数常常设置为10.

实际应用

目录，使用ReLU激活函数的，建议初始化为w = np.random.randn(n) * sqrt(2.0/n)，参考He et al

批归一化 Batch Normalization

这是个最近出现的技术，参考论文。它在一定程度上减轻了如何初始化网络权重的问题。具体做法为让数据在输入激活函数前先通过一个网络，通过这个网络之后，输出数据（即输入激活函数的数据）服从标准高斯分布。因为归一化是一个可以简单的求导操作，因此方案可行。实际应用中，常常在全连接层（卷积层）和激活函数(非线性操作）之间插入一个BatchNormalization层。批归一化可以理解为在网络每一层之前都做了预处理。

正则化

正则化用来阻止网络过拟合，有以下几种方法：

L2 regularization

L2正则化是最常用的方法；它可以直接惩罚目标函数中任何一个权重平方的幅度。具体实现时对于每一个权重$w$在目标函数都加上一项$\frac{1}{2}\lambda w^2$，其中$\lambda$常常等于$\frac{1}{2}$，这样方便求导运算。L2正则化可以直观理解为，它限制单个较大的权重，在权重和不变时，它把权重大概均匀分不到每个权重上。使用L2正则化后，在反向传播梯度更新时，权重会以W+=-lambda * W速度向0靠近。

L1 regularization

L1正则化也是常用的一种方法，在目标函数中，它给每个权重加上一项$\lambda |w|$。可以把L1和L2正则化结合起来$\lambda_1|w| + \lambda_2 w^2$（叫做Elastic net regularization）。L1正则化会使权重矩阵变得稀疏（非常接近0）；经过L1正则化后，使用时，用的就是输入的子集了（某些权重系数接近0，对应输入会变为0）。而L2正则化后，权重会变为大小分布均匀且都接近0的数。使用中，如果没有显示去选择特征，那么L2正则化效果一般优于L1正则化。

Max norm constraints

Max norm正则化限制梯度幅度最大值，并使用投影梯度来确保限制。使用中，参数更新方式不变，只需要检查更新后满足$||\overrightarrow{w}||_2 < c$，不满足则消减梯度。$c$常常设置为3或4。使用这个约束后，网络就不会“爆炸”，因为它限制了权重大小。

Dropout

Drop是非常简单高效的正则化方法，在论文Dropout: A Simple Way to Prevent Neural Networks from Overfitting 中介绍，可以作为上面正则化方法的补充。它的思想为在训练时，让神经元以概率$p$激活（或者设置为零，不激活）。

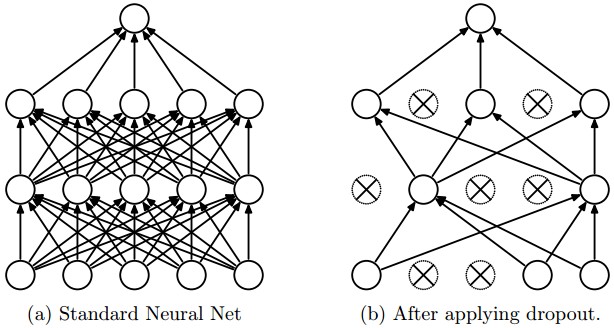
cs231n6_04.jpeg
例如上面图片中，左边是没有使用Dropout的网络，右边是使用了Dropout的网络。需要注意，Dropout只是在训练的时候使用，在测试时，不使用。

3层网络Dropout代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
""" Vanilla Dropout: Not recommended implementation (see notes below) """

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  """ X contains the data """
  
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p # first dropout mask
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # second dropout mask
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
  out = np.dot(W3, H2) + b3

在训练时使用了Dropout，在预测没有使用Dropout。在使用DropOut时，以概率$p$来激活神经元，那么一层网络的输出会变为原来的$p$倍；在预测是不使用DropOut，为了使得每一层输出值和训练时一致，在每一层计算后也要乘以概率$p$。

因为我们更加关心测试时的性能，在预测时增加计算会减低生产环境性能；一个解决的方法为在训练时，把使用DropOut的层除以概率$p$，这个方法叫做Inverted dropout。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
""" 
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)
  
def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b3

更多内容可以参考
Dropout paper by Srivastava et al. 2014.
Dropout Training as Adaptive Regularization: “we show that the dropout regularizer is first-order equivalent to an L2 regularizer applied after scaling the features by an estimate of the inverse diagonal Fisher information matrix”

Theme of noise in forward pass

DropOut是在前向传播时引入一些随机行为，在预测时通过数值方法补偿这个随机行为。这样类似的方法还有DropConnect。

Bias regularization

偏置不直接和输入数据相乘，它并不直接影响某一维度的数据，因此常常不用对偏置正则化。实际应用中，数据合理预处理后，对偏置正则化也很少导致算法性能变差；可能是因为权重系数远远多于偏置。

Per-layer regularization.

不同的层使用不同的正则化方法。很少见。

实践

1、全局使用L2正则化，$\lambda$大小通过交叉验证获得。
2、使用L2正则化后，常常再结合Dropout，一般可以设置$p=0.5$，也可以通过交叉验证获得。

损失函数

这里来讨论损失函数中的数据损失部分，在监督学习中常常用到，用来衡量预测值和真实值的差异程度。损失函数是输入数据的平均$L=\sum\frac{1}{N}_i L_i$，其中$N$是训练集大小。实际常常常常遇到以下几类问题

分类问题

这里假设每个样本都只有一个标签，最常用的两个损失函数为：

$$ L_i = \sum_{j\neq y_i} \max(0, f_j - f_{y_i} + 1) $$ $$ L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) $$

第一个是SVM分类中用到的，第二个时Softmax分类器用到的交叉熵loss。

Problem: Large number of classes.

当标签集合特别大时（例如单词字典等），要使用Hierarchical Softmax。其思想为，把标签构建为一棵树，每个标签为树的一条路径，在树的每个结点训练Softmax分类器。树的结构要依具体问题而定。

Attribute classification

如果一个样本的标签不止一个时，例如标签$y_i$是一个二值向量，可能包含标签集合中的某几个标签，且标签不互斥。这时可以为每个标签建立一个二值分类器:

$$ L_i = \sum_j \max(0, 1 - y_{ij} f_j) $$

$j$表示lable数量，$y{ij}$表示第$i$个样本是否包含第$j$个标签，如果包含$y{ij}$为+1，否则为-1；$f_i$表示预测值，正确预测时其值为正，否则为负。可以计算，当正确预测且分值小于1，或错误预测分值大于-1时，loss就会大于零。

还有一个方法，就是对每个标签训练一个分类器，那么loss函数为

$$ L_i = \sum_j y_{ij} \log(\sigma(f_j)) + (1 - y_{ij}) \log(1 - \sigma(f_j)) $$

这里$y_{ij}$是1（表示包含标签j）或0（不包含标签j）。

回归

对于预测连续值，回归问题的loss函数有L2正则化和L1正则化形式，分别为

$$ L_i = \Vert f - y_i \Vert_2^2 $$ $$ L_i = \Vert f - y_i \Vert_1 = \sum_j \mid f_j - (y_i)_j \mid $$

注意

1、与更加稳定的loss（例如Softmax）,L2 loss更加难以优化。L2 loss要求每个输入都要输出正确值；而Softmax的评分并不重要，只有当评分在适当量级时才有意义。
2、L2 Norm的鲁棒性并不好，异常值可能引起很大的梯度。
3、面对回归问题时，优先想想能不能转换为分类问题。
4、如果使用回归，L2是一个不错的选择。但是在dorpout网络结构中，不宜再用L2。

Structured prediction

结构化预测是指标签是任意的形状（树，图等），通常假设结构空间非常大且难以遍历。其思想和结构化SVM类似，在正确分类和分值最高的错误分类间建立一个分类面。

总结

1、数据预处理：零中心化，正则化把特征范围缩放为[-1,1]。
2、初始化权重方法，通过使用高斯分布，标准差为$\sqrt{2/n}$。
3、正则化L2,L1,Dropout。
4、BachNorm。
5、Loss函数

本文标题:cs231n-(5)神经网络-2：设置数据和Loss

文章作者:KangBing

发布时间:2016年09月24日 - 14时56分

最后更新:2018年12月19日 - 23时27分

原始链接:http://kangbing.github.io/2016/09/24/cs231n-(5)神经网络-2：设置数据和Loss/

许可协议: "署名-非商用-相同方式共享 3.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 数据预处理
    1. 1.1. 减去均值
    2. 1.2. 正则化
    3. 1.3. PCA and Whitening
  2. 2. 权重初始化
    1. 2.1. 全部初始化为零
    2. 2.2. 小的随机数
    3. 2.3. 校准方差
    4. 2.4. 稀疏初始化
    5. 2.5. 实际应用
    6. 2.6. 批归一化 Batch Normalization
  3. 3. 正则化
    1. 3.1. L2 regularization
    2. 3.2. L1 regularization
    3. 3.3. Max norm constraints
    4. 3.4. Dropout
    5. 3.5. Theme of noise in forward pass
    6. 3.6. Bias regularization
    7. 3.7. Per-layer regularization.
    8. 3.8. 实践
  4. 4. 损失函数
    1. 4.1. 分类问题
    2. 4.2. Problem: Large number of classes.
    3. 4.3. Attribute classification
    4. 4.4. 回归
    5. 4.5. 注意
    6. 4.6. Structured prediction
  5. 5. 总结
,
#add by kangyabing