梯度检查，参数更新，超参数优化和模型评估

梯度检查

梯度检查在理论上，对比推导的梯度和数值计算的梯度即可；在实践中，并不这么简单。

使用中心化形式的梯度计算

课本中都学过，梯度计算公式：

$h$一般是很小的值，实践中数量级为$1e-5$。

上面这种计算梯度公式实践中不常用，实践中常常用中心化形式：

这种中心化的形式，要求计算损失函数2次，带来的好处就是梯度精度提高了。可以使用泰勒级数展开验证，非中心化形式梯度计算公式误差为$O(h)$，中心化形式误差为$O(h^2)$

使用相对误差

数值梯度$f^{‘}_n$和推导梯度$f^{‘}_a$之间差异的对比，要比较两者的相对误差：

上面的分布上的$\max$运算可以替换为加法，这样可以避免分母为零的情况，但是也要注意两者绝对值都为零的情况。在实践中：

1、相对误差大于1e-2时，极可能梯度计算错误。
2、相对误差在1e-2和1e-4之间，有可能梯度计算错误。
3、相对误差小于1e-4，对于不光滑的激励函数来说可以接受；对于光滑激励函数（使用tanh nonlinearities和softmax），还是过高。
4、小于1e-7，一般来说是正确的。

注意，网络结果越深，梯度误差可能越大，因为在传播时误差会积累。例如一个10层的网络，相对误差为1e-2也可以接受；但是对于一个可导函数时，1e-2就不能接受了。

使用双精度

使用双精度将更加准确，有时单精度计算相对误差为1e-2，换成双精度后会变化1e-8。

数值范围要在单精度精确度内

读一下What Every Computer Scientist Should Know About Floating-Point Arithmetic会让你编码更加小心，减少错误。例如神经网络中，常常要对一个batch数据计算得到的loss函数进行归一化；如果loss函数本来就很小，进行归一化再去除以一个值，得到的归一化loss函数值将会更小，从而引起一系列问题。因此，常常需要把解析梯度和数值梯度的原始值打印出来，确保它们不是特别小。如果的确比较小，可以进行放大，一般放大的数值量级为1.0。

目标函数中的不连续点

梯度检查失败时，很可能是因为目标函数中的不连续点，函数ReLU、SVM loss、Maxout会引入不连续点。例如对于ReLU($\max(0,x)$)，$x=-1e-6$，$h>-1e-6$，那么$f(x+h)$和$f(x-h)$会在不连续点的两侧。
这不是极端情况，对于CIFAR-10，有50000个样本，每个样本有9个目标函数，那么总共有450000个$\max(0,x)$函数。

在计算梯度时，可以知道是否越过了不可导点。在前向传播时，记录$\max(x,y)$那个最大，在计算$f(x+h)$和f(x-h$时，如果至少有一个最大值发生变化，那么说明越过了不可导点。

使用少量数据点

使用数据点少，碰到上面不可导点的情况就少。使用数据点少，可以减小计算量，增快速度；如果只是检查2-3个点的梯度，那么可以检查整个batch的梯度。

注意h的大小

理论上$h$越小越好，但是实际中$h$不能太小，否则有数值问题，常常使用1e-4或1e-6。可以参考这里。

在典型mode检查

梯度检查只是在一些特定的点检查，即使这些点正确，放到全局也未必正确。尽可能选择典型mode检查梯度，例如svm训练，初始化后，不同类的score都接近0，这时最好不要检查梯度；果断事件，让网络学习一小段事件，loss函数下降之后在检查。

不要让正则化淹没数据

loss函数中有正则化的loss和data loss，在梯度检查时，不要让正则化的loss淹没了data loss。一种做法是在检查梯度时去掉正则化loss，检查正则化的梯度时，可以去掉data loss或增大正则化loss的权重。

关闭drop out和数据扩展

在检查梯度时，要去掉网络中的不确定因素，关掉drop out和数据扩展。关掉它们后，就无法对它们的正确性进行检查，一种更好的方法为在计算$f(x+h),f(x-h$前增加一个特定的随机种子，在计算推导梯度时也是如此。

检查少量维度

实践中，梯度可能有几百万个参，这种情况下，只需要检查几个维度，假设其他维度正确即可。但是要注意，要检查这些维度的每一个参数。例如，偏置数量很少，随机抽取可能检查不到偏置。

学习之前：合理检查的技巧

查看特定情况下的loss

当用小的值初始化参数时，确保期望的loss和实际loss一致。最好先去掉正则项，单独检查data loss。例如使用Softmax分类CIFAR-10时，初始化后得到的data loss应该是2.302（$-\ln(0.1)=2.302$）。对于SVM，初始时所有的score都为0，所以data loss为9。

增强正则化

增强正则化项时，loss增大。

过拟合一个小数据集

在进行全量数据训练前，使用一个小数据集训练（例如20个数据），去掉正则化项，这样可以确保得到loss值为0。即使在小数据集上得到loss为0，也未必完全正确。例如数据集是随机的，对于小数据集可以拟合，但是对于大数据集还是无法拟合。

观察训练过程

在训练过程中需要观察期过程，观察几个参数的变化过程。

训练过程中，日志往往记录着参数变化，可以将参数变化画成图，这样更加形象。横轴x一般表示epoch，用来衡量样本在训练中使用的次数，所有样本使用一次为1个epoch。有些使用迭代次数，需要注意的是迭代次数xbatchsize才是使用样本量。

Loss函数

第一个要观察的就是loss值的变化，它用来衡量一个batchsize的样本的前向传播。下图展示了loss值随时间变化，其形状可以得知学习率的情况：

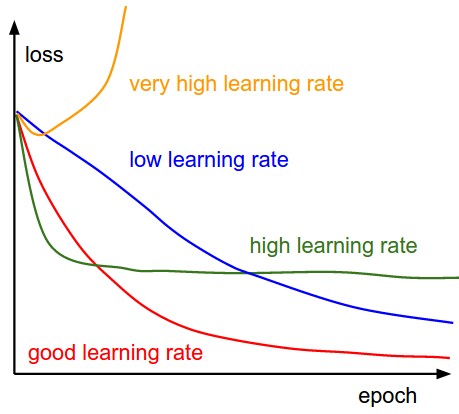
左边是一个示意图，学习率过低，学习效果时线性增长。高的学习率开始时学习效果时指数增长，但最后loss值在一个较高水平（绿色线）；这是因为在优化时，“能量”过大，导致参数震荡不能找到一个最优点。右边是实际训练中loss值随时间变化图，它是在CIFAR-10上训练的。这个loss值变化看起来比较合理（lr可能比较小，也难说），batchsize可能也比较小，因为loss的噪声比较大。

loss值的抖动和batch size有关。batch size太小，抖动会比较厉害。如果batch是整个训练集，loss值震动就会最小，因为每次更新的梯度都是最优。

也有人使用对数loss函数，因为学习过程可能是指数的，取对数后学习过程会像直线。如果有交叉验证模型，把结果画到同一副图上，这样它们之间差异会比较明显。

有时对数loss函数看起来很搞笑:lossfunctions.tumblr.com

训练/验证准确率

第二重要的就是观察在训练集和验证集上的准确率。这样可以直观得到模型是否过拟合。

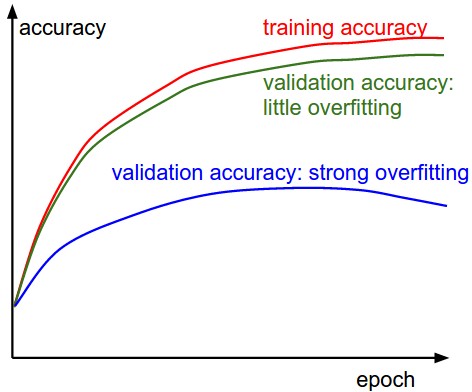
训练集和验证集上准确率之间的“间隔”可以衡量过拟合情况。蓝色线的验证集准确率和训练集准确率间隔过大，说明已经过拟合（验证集准确率可能在增长后还会下降）。在实践中遇到这种情况，一是加强正则化（更强的L2,更多的drop out），二是增大训练集。绿色线情况，验证集和训练集准确率变化完全一致，说明模型容量还不够大，增加参数来增加模型容量。

权重和更新的比例

最后要观察的是更新幅度和参数幅度之间的比值。注意，这里的更新不是原始梯度，例如在sgd中，是梯度乘以学习率。需要对每个参数及单独计算。这个比例的一个启发值是大概1e-3左右。如果太低，学习率太小，如果高学习率过大。下面是计算过程

1
2
3
4
5
6

# assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update # the actual update
print update_scale / param_scale # want ~1e-3

不是计算最大或最小值，而是计算和观察其范数的值。这些矩阵通常是相关的，也能得到近似的结果。

激活/每层梯度分布

参数的错误初始化会减慢学习速度，甚至使学习停止。这个问题比较容易解决，一种解决方法是画图每层梯度/激活函数的直方图。直觉上看，如果有奇怪的分布，那么可能就有问题。例如tanh神经元输出的直方图分布，应该可以看到参数在[-1,1]之间所有数值都有分布，但是如果全是0或者-1、+1，那么一般就是有问题了。

第一层可视化
如果使用像素数据，那么可视化第一层可能会有帮助：

左边的图中有许多噪声，网络没有收敛，可能是学习率或正则化的问题。右边的图比较平滑、干净、特征比较多，说明学习过程很好。

参数更新

在反向传播中计算好解析梯度，使用解析梯度更新参数，有不同的方法来更新参数。

神经网络的优化是当前非常热额研究热点。本文只是讲解实践中常常用到的技巧，给出直观上的解释。如果需要了解细节，我们提供了额外读物。

SGD and bells and whistles

Vanilla update
最简单的更新就是沿着梯度负方向更新。夹着x是参数向量，dx是梯度向量

1
2

# Vanilla update
x += - learning_rate * dx

这里learning_rate是一个超参数，它是固定值。当使用这个训练集，且学习率足够小，就可以降低loss函数值。

Momentum update

Momentum更新在深度网络中总能有更好的收敛速度。这种更新方式可以从物理优化角度来解释。loss值看一看到山的高度（有高度就有势能$U=mgh$， 且$U \propto h$）。用随机数初始化参数等价于设置质点在某位置的速度为0；优化过程可以看做参数向量（即质点）滚动的过程。

因为质点所受的力和势能的梯度相关（$F = - \nabla U$），质点所受的力是loss函数的负梯度。有$F=ma$，所以负梯度和质点的加速度成正比。这个观点和SGD不同，SGD是直接合并位置；而物理学观点是梯度只是影响速度，速度影响位置。

1
2
3

# Momentum update
v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position

这里引入了参数v，初始化为0，还引入了参数mu。说的不恰当一些，这个参数可以当做动量(momentum，常常设置为0.9），它的物理意义是和摩擦力一致。这个变量减小了速度，降低了系统的势能，否则质点在山底也不会停下来。使用交叉验证时，这个参数可以设置为$[0.5, 0.9. 0.95. 0.95]$。和学习率退火时间类似，动量随时间设置不同值可以略微改善优化效果，动量在学习后阶段可以增大。一个典型的设置是在初始时设置为0.5，后面随着epoch增大，直至到0.99.

随着动量更新，参数会在有梯度的方向上增加速度。

Nesterov Momentum

Nesterov Momentum和标准的Momentum有点不同，对于凸优化，在理论上它能有更好的收敛，在实践中，它的性能优于标准momentum。

Nesterov Momentum的核心思想是，当参数向量在位置x时，回看一下momentum更新，只考虑动量部分（忽略第二项梯度部分），通过mv*v影响参数。当我们打算计算梯度梯度时，把未来一个近似位置x+mu*v当做“向前看”-这个点是将来更新后位置的附近，计算这个点x+mu*v的梯度，而不是旧位置x。

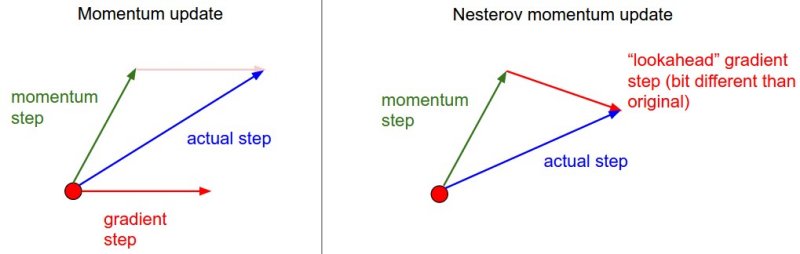
左边是标准的Momentum update，右边是Nesterov momentum update。红色的点是“旧位置”。

实现如下:

1
2
3
4

x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

在实践中，人们更喜欢类似标准SGD或momentum update的形式。可以通过参数x_ahead=x+m*v改写实现，用x_ahead表示更新，不用x。即实际中计算时总是计算前一步的版本。公式中x_ahead（改回x）变为：

1
2
3

v_prev = v # back this up
v = mu * v - learning_rate * dx # velocity update stays the same
x += -mu * v_prev + (1 + mu) * v # position update changes form

我们推荐阅读公式来源和数学推导Nesterov’s Accelerated Momentum(NAG):

Advances in optimizing Recurrent Networks by Yoshua Bengio, Section 3.5.
Ilya Sutskever’s thesis (pdf) contains a longer exposition of the topic in section 7.2

Annealing the learning rate

在训练深度网络过程中，要学会对学习率退火。如果学习率太高，系统就有太大的动能，参数在某一范围内波动，loss函数不能到达更窄更深的位置。合适减小学习率是有技巧的，如果减小太慢，loss函数值会一直某一范围波动，提高很少，这样浪费计算资源；如果减小太快，系统动能很快降了下来，将不能到达最好的位置。常常用到的退火策略有以下三种：

Step decay
经过几个epoch，就降低学习率。典型值为讲过5个epoch就减小为一半，或经过20个epochs变为原来的0.1倍。当然这些具体值要依具体问题和模型而定。一个启发式的做法是在实践训练中观察交叉验证集的错误率，入股错误率停止增大，学习率乘以一个常量（例如0.5）。

Exponential decay
数学形式为$\alpha = \alpha_0 e^{-k t}$，其中$\alpha_0,k$是超参数，$t$是迭代。

1/t decay
数学形式为$\alpha = \alpha_0 / (1 + k t )$，其中$\alpha_0,k$是超参数，$t$是迭代。

Second order methods

还有一类优化的方法，主要是基于Newton’s method，它的迭代形式为:

其中$H f(x)$是Hessian matrix，它是函数二阶偏导数组成的方阵。$\nabla f(x)$是梯度向量。直观上看，Hessian matrix描述了loss函数的局部曲率，局部曲率可以更我们更高效的更新参数。乘以Hessian matrix的转置，在曲率小时大步前进，在曲率大时小步前进。注意，上面更新中没有学习率，这正是比一阶导数有优势的地方。

二阶导数虽然理论上更加有效，但是实际中很少用到。因为矩阵求逆计算量太大，且占用太多内存。对于Hessian矩阵求逆也有一些研究实际中有一些计算近似的方法，例如L-BFGS，具体内容可以参考

Large Scale Distributed Deep Networks is a paper from the Google Brain team, comparing L-BFGS and SGD variants in large-scale distributed optimization.
SFO algorithm strives to combine the advantages of SGD with advantages of L-BFGS.

Per-parameter adaptive learning rate methods

前面的所有方法都是对所有参数同时使用。调优学习率是昂贵的过程，因此许多工作投入到自适应学习率，甚至每个参数适应学习率。虽然很多方法需要设置其他超参数，但是这些超参数在比较大的变化范围上，不会太影响系统性能，但是原始学习率会影响。下面，介绍一些在实践中常常用到的自适应算法。

Adagrad
Adagrad是由Duchi et al..提出，实现如下

1
2
3

# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

cache和dx大小相同，跟踪每个参数的平方和，用来归一化参数更新，需要注意它是element-wise。从代码中可以看出，如果梯度大，那么将会减小学习率；如果梯度小，将会增大学习率。求平方根操作非常重要，没有它算法效果将会非常差。平滑项eps（范围通常为1e-4到1e-8）可以避免分母为零。Adagrad的缺点是在深度学习中，单调的学习率被证明通常是太激进，很早就使得学习停止了。

RMSprop
RMSprop是非常高效但是没有公开发表的自适应学习率的方法。它是Adagrad方法的修改版，减小它的集锦性，单调减小学习率。尤其是它使用了梯度平方的滑动平均。

1
2

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

其中decay_rate是超参数，其值一般为[0.9, 0.99, 0.999]。x+=更新部分和Adagrad相同，但是cache变量部分不同。RMSProp依然是基于梯度大小对学习率进行调节，有不错的效果，和Adagrad不同的是，它不会单调递减学习率。

Adam
Adam是最近提出的，有点像带有动量的RMSProp，它的精简版更新如下：

1
2
3

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

注意到其更新非常像RMSProp，不同点是这里使用的是平滑版本的梯度m，而不是原始梯度dx。论文中推荐参数的值eps=1e-8,beta1=0.9,'beta2=0.999。实践中，推荐默认使用Adam，它的效果往往好于RMSProp；但是也推荐尝试一下SGD+Nesterov Momentum。完整的Adam更新包括偏置矫正机制，因为向量m,v在前几步中初始化，因此网络“热身”之前，偏置为零。了解更多细节，参考论文或课外读物。

课外读物：
Unit Tests for Stochastic Optimization proposes a series of tests as a standardized benchmark for stochastic optimization.

通过下面两张动画可以直观感受不同优化算法：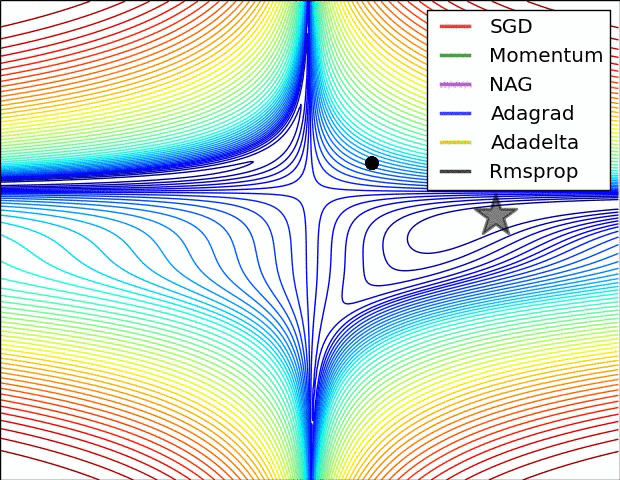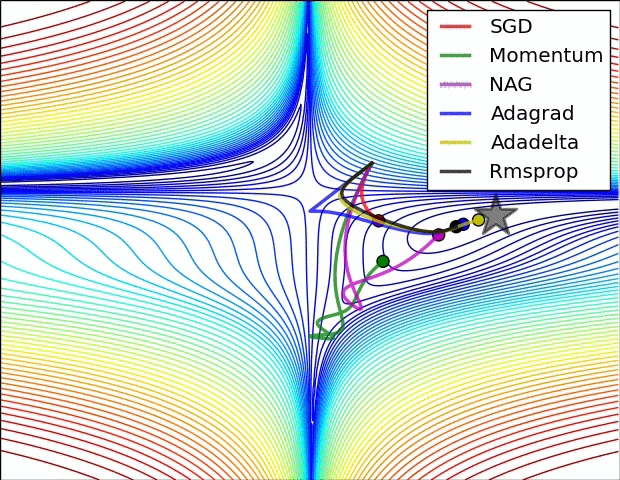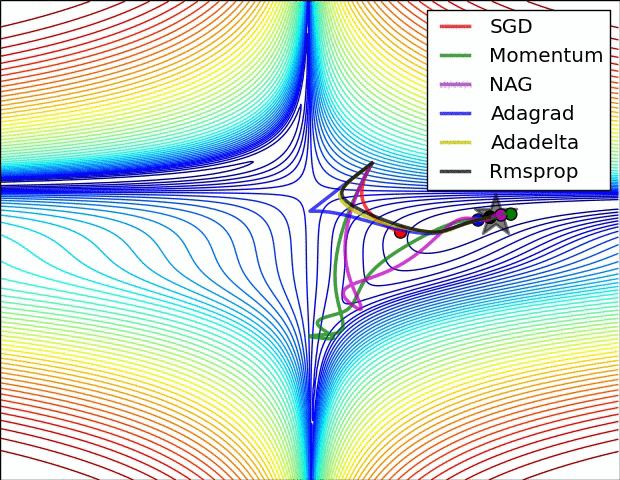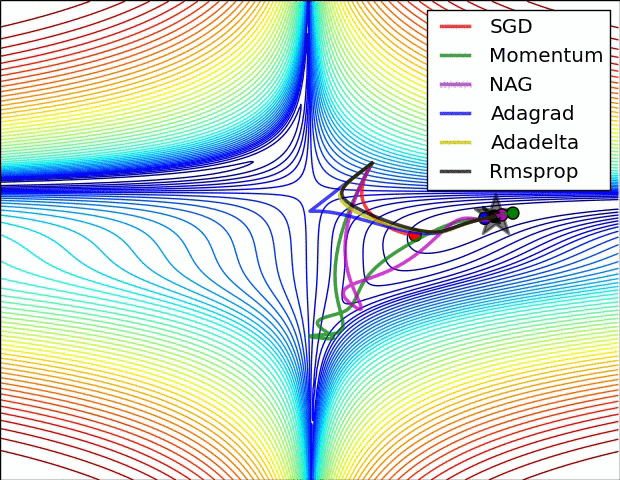

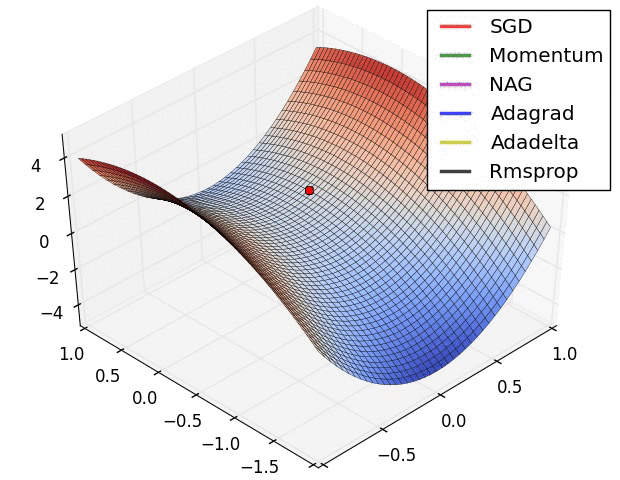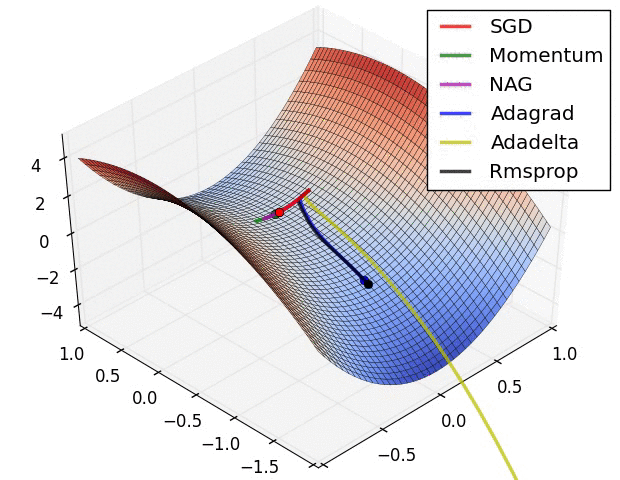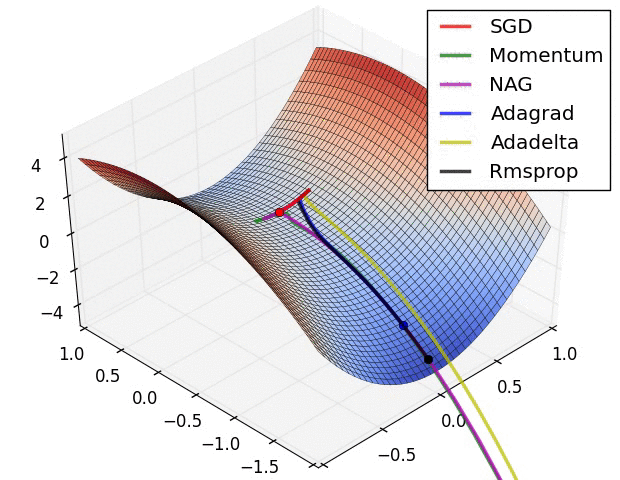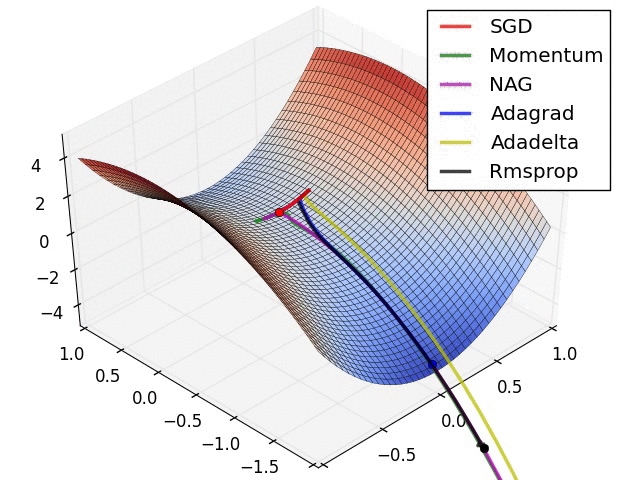
上面图片是loss函数的等高线。注意到带有动量的方法，一旦走偏，很难纠正回来，它的线路就行小球向下滚。下面图片是带有鞍点的图形，某些维度开口向上，某位维度开口向下。注意到SGD方法很难突破对称性的限制，被困在了高点。与此相反的是，像RMSprop这样的算法可以看到鞍点更低的梯度；因为更新过程中分母选项的原因，将会增大这个方向的学习率，帮助RMSProp在这个方向前进。

超参数优化

训练神经网络包括许多超参数集，神经网络中最常见的包括：
1、初始化学习率
2、学习率衰减算法（例如常量衰减）
3、正则化强度（L2，dropout 强度）

还有一些相对弱一些的超参数（神经网络不那么敏感），例如per-parameter adaptive learning method， 动量及其设置。这一小节，讲解调参的额外方法和技巧。

实现

大的神经网络需要很长时间来训练，调参可能需要几天甚至几周。设置代码时，要有一个worker连续随机设置参数，之后优化。在训练时worker在完成一个epoch后，测试在验证集上的性能，且保存check point到文件，文件中要有在验证集上性能的信息。还要有一个master程序，用来管理worker程序，还可以检查check point，记录训练过程等。

优先选用一个验证集，而不是交叉验证

在大多场景中，使用大小合适的验证集可以让代码简单，没必要使用多折交叉验证。可能常常听说用交叉验证集来设置超参数，在大多情况下，只是使用了一个验证集。

超参数的范围

以对数为尺度来设置超参数。例如，学习率取样范围learning_rate = 10**uniform(-6,1)；即学习率是10的指数幂，幂的大小(-6,1)上的随机数。这个策略也适用于正则化强度。这是因为学习率和正则化强度是乘的影响，因为对于它们值的范围取值，乘以或除以某个数，而不是加上或减去某个数。但是有些超参数（drop out）是在原有尺度进行设置，dropout=unifor(0,1)。

优先使用随机搜索，而不是网格搜索

论证过程参考 Random Search for Hyper-Parameter Optimization。原理大概为，超参数中，一些超参数比另一些重要，因此随机搜索更有可能找到更优的超参数。

对边界上的最优值格外小心

边界上的最优值可能不是全局最优。例如，对于学习率，其范围learning_rate = 10 ** uniform(-6, 1)，最终使用的学习率不应该出现在边界处，如果时，要扩大范围来进一步搜索。

由粗到细来搜索

实践中，现在一个大范围搜索，之后逐步缩小搜索范围。在大范围搜索时，只需要一个或半个epoch即可，因为某些不合适的超参数极有可能让网络学不到任何东西，甚至引起loss值爆炸。在细搜时，让训练运行5个左右的epoch，缩小范围后，还可以进一步细搜，直到找到最优值。

贝叶斯超参数优化

贝叶斯超参数优化是专注于超参数空间更高效导航算法的研究领域。其核心思想是在探索上找平衡–探索和不同超参数设置之间的平衡。在此基础上开发出一些库。但是在卷积网络实践中，找一个范围认真设置的性能一般很难超越随机搜索。这里有更详细的讨论。

评估

模集成

在实践中，可以把性能提升几个百分点的一种方法是：训练多个独立的模型，在测试时把多个模型的结果求平均。随着模型数量增大，性能会单调递增，但是越到后面提升越少。不同模型越是多样性，性能提升越是明显。有以下几种方式集成：

同一个模型，不同初始化
使用交叉验证找到最优的超参数。使用最优超参数、不同初始化方式来训练。这种方式缺点是它仅仅依靠不同初始化。

交叉验证选择最优模型
使用交叉验证找到最优模型，选择最优参数的前几个（例如10个）来做模型集成，增加模型的多样性。这样可能会把次优模型包含进来。这种方式比较容易实践，因为它在交叉验证后不需要再训练了。

同一个模型，不同记录点
训练过程中，随着时间进行，每个epoch都保存一个模型，这样就会有多个模型，使用这些模型来集成。这样虽然缺少多样性，但是在实践中也有良好性能。优点是这种方式代价很小。

训练时运行参数的平均值
和上一个方法相关，一种代价很小，但是可以提升模型一两个百分点的方法：训练时在内存保存参数的拷贝，当loss函数出现指数下降时，记录这个参数；最终使用记录这些参数的平均。这个平滑版本的参数在验证集上有更小的误差。一个直观理解为目标函数是碗状的，参数在碗的周边跳跃，参数的平均更有可能到达碗的更深处。

模型集成的缺点就是测试单个样本时，计算量增大了。Geoff Hinton的论文Dark Konwledge提出集成模型为单个模型的方法，通过修改目标函数，加入似然函数来实现。

总结

训练一个神经网络
1、梯度检查，使用小批量数据。
2、合理性检查，确保初始化的loss合理，过拟合小数据集，在小的训练集上达到100%准确率。
3、训练时，监督loss，训练集/验证集准确率。参数更新幅度和参数值比值应该在1e-3附近；如果训练神经网络，可视化第一层权重。
4、推荐使用的2种更新方法：SGD+Nesterov Momentum or Adam。
5、训练不同阶段，减小学习率。例如，固定几个epoch后降低或验证集识别率停止后降低。
6、随机搜索超参数（不是网格搜索），分阶段搜索（1-5个epoch在大的范围搜索，之后搜索范围）。
7、使用模型集成得到额外提升。

拓展参考

SGD tips and tricks from Leon Bottou
Efficient BackProp (pdf) from Yann LeCun
Practical Recommendations for Gradient-Based Training of Deep Architectures from Yoshua Bengio