cs231n-(6)实现Minimal神经网络

cs231n笔记

本节将实现一个神经网络。首先将实现一个线性分类器，之后扩展到实现一个2层的神经网络。

生成数据

首先来生成线性不太容易可分的数据集。下面生成一个螺旋结构的样本集，生成过程和画圆类似，只是半径在依次增大，角度加上了一个随机噪声

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
import matplotlib.pyplot as plt
N = 100 # 每类样本个数
D = 2 # 维度
K = 3 # 类别数
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in xrange(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # 半径
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # 角度，加上是一个随机噪声
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
%matplotlib inline
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral

生成结果如下：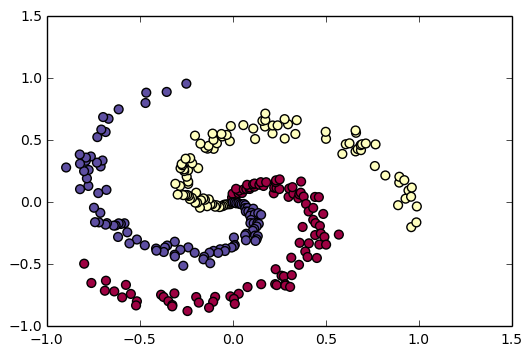
cs231n07_01.png
样本有三种颜色：蓝、红、黄，它们之间是线性不可分的。

一般情况下，我们要对数据进行预处理，让每个特征的数据均值为零，方差为1。上面生成的数据值范围为(-1,1)，因此跳过数据预处理这一步。

训练Softmax线性分类器

训练一个Softmax线性分类器来分类来分类这些数据。Softmax线性分类有一个分值函数用来评价每个类别的得分，一个交叉熵损失函数用来计算loss。

初始化参数

线性分类器包含一个权重矩阵W和偏置向量b，用随机数初始化它们

1
2
3
# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

计算分值

可以用矩阵相乘计算分值

1
scores = np.dot(X,W) + b

上面生成的数据为300个2为数据，所以scores大小为[300x3]，每一行是一个样本对应3类的分值。

计算loss

需要定义一个loss函数，这个函数可导，用来衡量分值的匹配情况。直观上看，我们想要正确的类别分值高，错误的类别分值低；有许多方法可以量化这个分类标准，本节使用交叉熵loss。$f$是分值数组，每个元素对应某一类别的分值，那么Softmax分类器计算loss：

$$ L_i = - \log(\frac{e^{f_{y_i}}}{\sum_j e^{f_j}}) $$

Softmax分类器把分值先进行归一化，得到概率，再取对数、取反，得到loss值。可以看出，概率越大，对应的loss值越小。

Loss一般由data loss和正则化loss组成

$$ L = \underbrace{ \frac{1}{N} \sum_i L_i }_\text{data loss} + \underbrace{ \frac{1}{2} \lambda \sum_k\sum_l W_{k,l}^2 }_\text{regularization loss} \\\\ $$

的到上面的scores后，我们首先计算概率

1
2
3
4
# get unnormalized probabilities
exp_scores = np.exp(scores)
# normalize them for each example
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)

得到的概率probs已经归一化，大小为[300 x 3]，每一行对应3个类别的得分。下面计算正确类别的log对数

1
corect_logprobs = -np.log(probs[range(num_examples),y])

corect_logprobs是一维的向量，对应正确类别的loss。最终的loss是data loss的平均加上正则化losss

1
2
3
4
# compute the loss: average cross-entropy loss and regularization
data_loss = np.sum(corect_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss

上面代码中，正则化强度$\lambda$包含在reg中。在训练开始时，很可能loss = 1.1，即等于np.log(1.0/3)，初始时每一类得分可能会很接近。

计算方向传播的分析梯度

我们已经有了评估loss的方法，现在要做的就是最小化它。下面使用梯度下降法。引入中间变量$p$，它是归一化后的概率向量

$$ p_k = \frac{e^{f_k}}{ \sum_j e^{f_j} } \hspace{1in} L_i =-\log\left(p_{y_i}\right) $$

现在要理解，计算得到的分值$f$怎样才能减小loss$L_i$。即求导数$\partial L_i / \partial f_k$，$L_i$由$p$计算得到，$p$依赖$f$

$$ \frac{\partial L_i }{ \partial f_k } = p_k - \mathbb{1}(y_i = k) $$

假设 p=[0.2 ,0.3, 0.5]，正确类别对应的得分为0.3，根据上面的公式，求导后结果为df=[0.2, -0.7, 0.5]。直观上看，中间元素导数为负，增加中间的得分，loss函数就会减小。
prob每行存储每个样本对应类别的分值，计算分值的梯度dscores：

1
2
3
dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples

分值是由scores = np.dot(X, W) + b计算得到，计算权重和偏置的导数

1
2
3
dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # don't forget the regularization gradient

使用矩阵相乘计算反向传播，不要忘记正则化的导数

执行更新

向梯度反方向前进

1
2
3
# perform a parameter update
W += -step_size * dW
b += -step_size * db

最终整合：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in xrange(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
#Train a Linear Classifier

# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in xrange(200):
  
  # evaluate class scores, [N x K]
  scores = np.dot(X, W) + b 
  
  # compute the class probabilities
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
  
  # compute the loss: average cross-entropy loss and regularization
  corect_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(corect_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W)
  loss = data_loss + reg_loss
  if i % 10 == 0:
    print "iteration %d: loss %f" % (i, loss)
  
  # compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples
  
  # backpropate the gradient to the parameters (W,b)
  dW = np.dot(X.T, dscores)
  db = np.sum(dscores, axis=0, keepdims=True)
  
  dW += reg*W # regularization gradient
  
  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db

得到输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
iteration 0: loss 1.098499
iteration 10: loss 0.905020
iteration 20: loss 0.833327
iteration 30: loss 0.800789
iteration 40: loss 0.783818
iteration 50: loss 0.774114
iteration 60: loss 0.768204
iteration 70: loss 0.764437
iteration 80: loss 0.761952
iteration 90: loss 0.760271
iteration 100: loss 0.759109
iteration 110: loss 0.758293
iteration 120: loss 0.757712
iteration 130: loss 0.757294
iteration 140: loss 0.756990
iteration 150: loss 0.756768
iteration 160: loss 0.756604
iteration 170: loss 0.756483
iteration 180: loss 0.756393
iteration 190: loss 0.756326

运行完之后，可以测试准确率

1
2
3
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))

得到：

1
training accuracy: 0.52

可以看出，线性分类器并不能很好的分类。可视化分类边界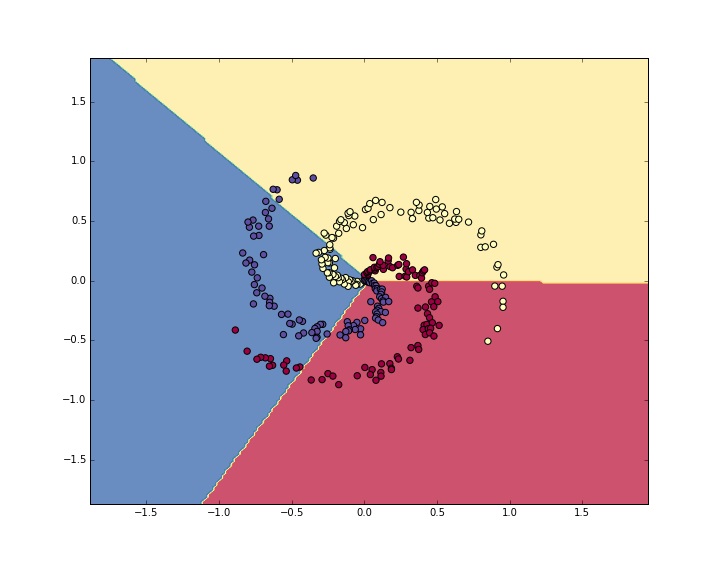
cs231n07_02.png

训练神经网络分类器

线性分类器不能很好的分类这些数据，下面使用神经网络来分类。一个隐藏层就可以分好分类这些数据（增加了非线性），需要训练两层网络的参数。

和前面线性分类器不同的是，第一层输出经过ReLU后输入到隐藏层，之后输出。ReLU表达式为
$$ r = max(0,x) $$

那么求导时，变为：
$$ \frac{dr}{dx}=1(x>0) $$
可以看出，如果输入大于0，那么允许梯度通过，否则不允许梯度通过。
训练好之后，评估网络的性能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
import  numpy as np

N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in xrange(K):
  ix = range(N*j,N*(j+1))
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
  y[ix] = j

# initialize parameters randomly
h = 100  # size of hidden layer
W = 0.01 * np.random.randn(D, h)
b = np.zeros((1, h))
W2 = 0.01 * np.random.randn(h, K)
b2 = np.zeros((1, K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3  # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in xrange(10000):

    # evaluate class scores, [N x K]
    hidden_layer = np.maximum(0, np.dot(X, W) + b)  # note, ReLU activation
    scores = np.dot(hidden_layer, W2) + b2

    # compute the class probabilities
    exp_scores = np.exp(scores)
    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)  # [N x K]

    # compute the loss: average cross-entropy loss and regularization
    corect_logprobs = -np.log(probs[range(num_examples), y])
    data_loss = np.sum(corect_logprobs) / num_examples
    reg_loss = 0.5 * reg * np.sum(W * W) + 0.5 * reg * np.sum(W2 * W2)
    loss = data_loss + reg_loss
    if i % 1000 == 0:
        print "iteration %d: loss %f" % (i, loss)

    # compute the gradient on scores
    dscores = probs
    dscores[range(num_examples), y] -= 1
    dscores /= num_examples

    # backpropate the gradient to the parameters
    # first backprop into parameters W2 and b2
    dW2 = np.dot(hidden_layer.T, dscores)
    db2 = np.sum(dscores, axis=0, keepdims=True)
    # next backprop into hidden layer
    dhidden = np.dot(dscores, W2.T)
    # backprop the ReLU non-linearity
    dhidden[hidden_layer <= 0] = 0
    # finally into W,b
    dW = np.dot(X.T, dhidden)
    db = np.sum(dhidden, axis=0, keepdims=True)

    # add regularization gradient contribution
    dW2 += reg * W2
    dW += reg * W

    # perform a parameter update
    W += -step_size * dW
    b += -step_size * db
    W2 += -step_size * dW2
    b2 += -step_size * db2
# evaluate training set accuracy
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print 'training accuracy: %.2f' % (np.mean(predicted_class == y))

得到输出：

1
2
3
4
5
6
7
8
9
10
11
iteration 0: loss 1.098731
iteration 1000: loss 0.354729
iteration 2000: loss 0.276981
iteration 3000: loss 0.246608
iteration 4000: loss 0.247844
iteration 5000: loss 0.245945
iteration 6000: loss 0.246020
iteration 7000: loss 0.245587
iteration 8000: loss 0.245091
iteration 9000: loss 0.244915
training accuracy: 0.98

可视化神经网络分类边界：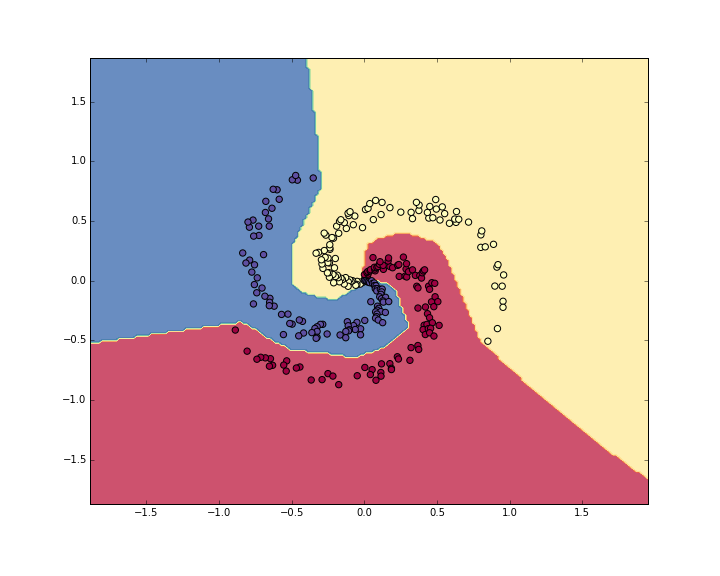
cs231n07_03.png

总结

使用很简单的2维数据训练线性分类器和2层神经网络，可以看出，从线性分类器改为神经网络只需要很简单修改，但是性能有极大提升。

参考： IPython Notebook code

本文标题:cs231n-(6)实现Minimal神经网络

文章作者:KangBing

发布时间:2017年02月18日 - 21时46分

最后更新:2018年12月19日 - 23时27分

原始链接:http://kangbing.github.io/2017/02/18/cs231n-(6)实现Minimal神经网络/

许可协议: "署名-非商用-相同方式共享 3.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 生成数据
  2. 2. 训练Softmax线性分类器
    1. 2.1. 初始化参数
    2. 2.2. 计算分值
    3. 2.3. 计算loss
    4. 2.4. 计算方向传播的分析梯度
    5. 2.5. 执行更新
  3. 3. 训练神经网络分类器
  4. 4. 总结
,
#add by kangyabing