讲解网络的各种层

卷积神经网络和普通神经网络非常类似。卷积神经网络由神经元组成，每个神经元包含权重weight和谝置bias；它接收上一层输入，和权重相乘，通常再经过一个非线性函数（可选）输出。整个网络拟合一个可微分的score function:从原始图像到每类别得分。在最后一层（全连接层）包含一个loss function（例如SVM/Softmax），常规神经网络用到的技巧，卷积神经网络通常也适用。

架构总览

上一节用到的网络是全连接网络，它接收一个向量输入，得到每个类别的得分。全卷积网络不太适用于图像，在CIFAR-10中，图像大小是32x32x3，所以第一层网络的每个神经元将会有32323=3072个权重；当输入图像变大后，权重数量会以乘积形式增长；神经元的数量不止一个，这么多的权重，将会导致过拟合。

3维神经元。图像由三个维度组成：width、height、channel，因此“层”也是对应三维：width、height、depth，这里的depth是激活函数的维度，不是神经网络的depth。

卷积神经网络和全连接网络的不同在于，卷积神经网络只是用全一层的部分输出作为一个神经元的输入，这样可以大大减少权重个数。下面是可视化的一个对比：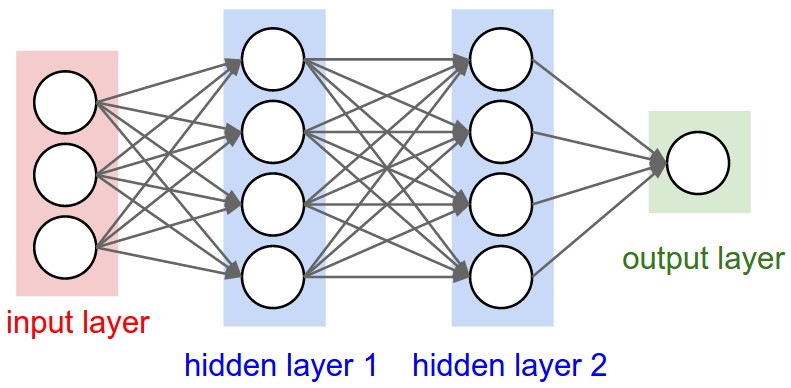

左边是3层的全连接网络。右边是卷积神经网络，把神经元按照三维来组织的。

常用的层

卷积神经网络由层构成，每层有简单的接口：把输入的三维数据转换为输出的三维数据，通常使用可微函数或者不用参数。

卷积网络由一系列的层构成，数据在层之间流动。常用到的层包括：卷基层Convolutional Layer、池化层Pooling Layer、全连接层Fully-Connected Layer。

以一个分类CIFAR-10图像的卷积网络为例，网络结构[INPUT-CONV-RELU-POOL-FC]，具体如下：

• INPUT[32x32x3]，数据为原始像素值，高宽都为32，三通道RGB。

• CONV layer，卷积层计算对象连接到输入层神经元的输出，每次计算都是权重和局部输入的点乘。如果使用12个滤波器（核），输出为[32x32x12]。

• RELU layer，ReLU是逐元素操作（elementwise），使用函数$max(0,x)$，经过ReLU后，输出大小不会变，还是[32x32x3]。

• POOL layer，池化层是下采样操作（在宽weight和高height纬度上），这样输出会变小为[16x16x12]，但是depth不变。

• FC layer全连接层将会计算每类别对应的得分，输出大小为[1x1x10]，代表10类每个类别的得分。全连接顾名思义，这一层的每个神经元和上一层的每个神经元之间都有连接。

通过上面的网络，把原始像素值通过不同的层，最终得到每个类别的得分。上面的层中，卷积层和全连接层有参数，池化层没有传参数，训练是训练有参数的层。

总结：

• 卷积网络最简单的结构就是一系列的层的连接，把输入的图像转换为输出。
• 有不同类型的层，最常用的有CONV/FC/RELU/POOL。
• 每个层都是接收三维数据，之后通过一个可微函数转换成一个三维输出。
• 层可以包含参数，也可以不包含。
• 层可以包含超参数，也可以不包含。

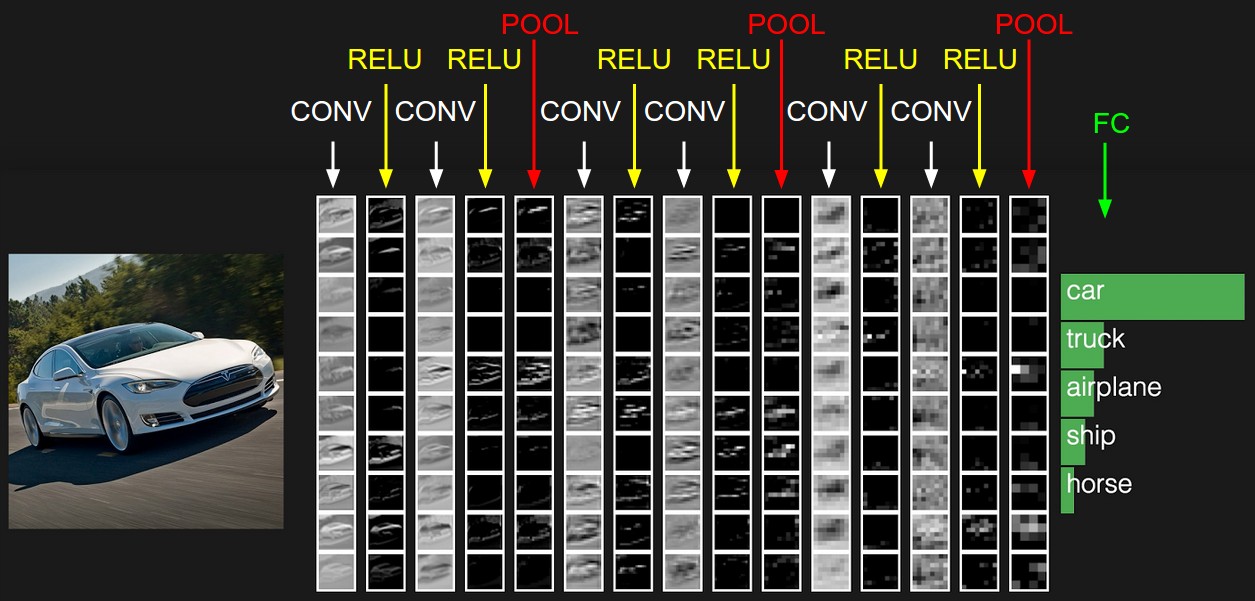
上图就是一个卷积网络的可视化，因为对三维数据难以可视化，对三维数据通过行来切片平铺展示，最后一层是对应每类的得分。这个网络是tiny VGG NET。

下面详细介绍每种类别的层的结构。

卷积层

卷积层是卷积网络的核心，大部分的计算量都在这个层。

概述

不考虑和大脑、神经元做对比，卷积层参数包含要学习参数的一个集合。每个滤波器参数长度和宽度比较小，但是深度和输入数据保持一致。在前向传播过程中，把卷积核沿着输入数据在宽和高上滑动，把对应的数据和卷积核做内积运算；随着卷积核的滑动，可以得到一个2维的激活图（activation map），激活图的值是卷积核在不同空间位置的响应。直观上看，网络会让卷积核学到“对某些特定物体或颜色产生激活”。假设我们有一个卷积核的集合，每个卷积核都会生成一个2维激活图，多个卷积核就可以在深度方向上得到输出。

大脑角度，从大脑角度看，每个3维输出可以看做一个神经元的输出，每个神经元只是观察到了输入数据的一部分，在空间上和左右两边的神经元进行参数共享。

局部连接，每个神经元只跟前一层输入的一个局部区域相连接；这个局部区域大型是一个超参数，叫做感受视野receptive field，其大小就是卷积核大小，其深度和输入数据深度一致。

例如，对于RGB CIFAR-10的图像，如果感受视野（卷积核/滤波器）大小为5x5，那么权重大小为[5x5x3]，总共有参数553+1=76个（加上一个bias）。

如果输入数据大小为[16x16x20]，感受视野（卷积核）3x3，那么权重为[3x3x20]。

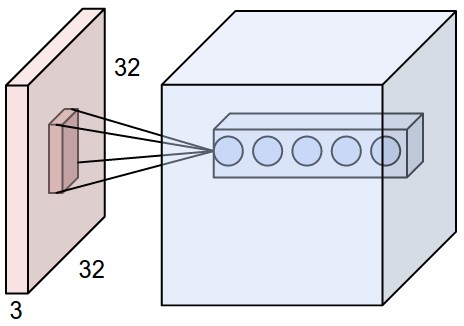
左图是32x32x3(CIFAR-10)的一个输入，卷积核只是连接到输入的局部部分，但是扩展到输入的整个深度。右边是一个神经元，它计算输入数据和权重的内积，再加上一个bias；随后经过一个非线性函数。

空间安排，前面已经解释了输入数据如何跟输出进行连接，但是还没讨论神经元的数量以及它们之间如何排列，这里需要用到三个超参数:深度depth，步长stride，零填充zero-padding：

1、输出的深度对应卷积核的个数，不同的卷积核查找输入中不同的物体。例如，输入是原始图像，那么深度方向上不同神经元可能被颜色、边缘、特定形状所激活。沿着深度方向上排列的叫做深度列depth column。

2、步长是卷积核滑动的距离，例如stride=1表示滑动一个像素；stride=2卷积核会滑动2个像素，这样得到的输出width和height会比输入小。

3、有时候，在输入的边缘上填充0会给计算带来方便，这种操作叫做零填充zero-padding。零填充的大小也是一个超参数，其大小会影响输出在空间上的大小（常常用来填充，使得输入和输入的width和height大小一致）

计算输出在空间的大小，输入的size为W，卷积核size为F，步长为S，零填充为P，那么输出的size为（W - F + 2P）/ S +　１。例如输入为7x7，卷积核3x3，零填充为0，步长为1，那么输入大小为5x5；如果步长为2，那么输出大小为3x3。

上图是沿着某一维度的例子，输入是7x7，卷积核是3x3（最右边），bias为零；左边stride=1，中间stride=2。注意（W - F + 2P）/ S一点要可以整除。

权重在同一个输入的激活图上，是共享的。

零填充的使用：上面的例子中，输出的size比输入小，如果使用零填充P = (F - 1)/2，那么输出和输出size大小将一致。

步长的限制：超参数有一些限制。例如，W = 10, P = 10, F = 3，那么步长S = 2就不合适，因为(W - F + 2P)/S + 1 = (10 − 3 + 0) / 2 + 1 = 4.5，不是整数，这将导致神经元不能整齐滑过输入数据。这样的参数被认为是无效的。卷积网络库可能会报异常，或者通过零填充/裁剪来使大小合理。

实际例子：AlexNet输入大小为[227x227x3]，第一个卷积层F=11,S=4,P=0，(227-11)/4+1=55，第一个卷积层depthK=96，所有共有96个卷积核，每个卷积核[11x11x3]。

参数共享，参数共享可以减少参数个数。以AlexNet第一个卷积层为例，共有神经元555596=290,400，如果不适用参数共享，每个神经元有11113=363个权重和1个bias，共有参数290400*364=105,705,600 个。

可以基于几个假设来减少参数：如果计算位置(x,y)处的某一特征的卷积核，应该可以计算不同位置(x2,y2)处的相同特征，所以可以使用同一个卷积核。即可以在深度方向上做一个2维切片（depth slice），每个切片使用相同权重。这样AlexNet第一层就有961111*3=34,848个权重和96个bias。在反向传播时，要计算每个神经元都权重的梯度，这样要在一个深度切片上进行累加，更新时，单独更新每一个深度切片对应的权重。

注意，如果在一个深度切片上使用相同的权重，那么前向传播就是输入数据和权重的卷积运算（卷积层名字的由来），这也是为什么称权重为滤波器或卷积核。

上图是AlexNet第一个卷积层权重[11x11x3]的可视化，对应96个不同卷积核，每个权重用来计算[55x55]个神经元。注意到参数共享是合理的：如果检测某一位置水平方向边界很重要，那么也应该适用于其他地方，因为具有平移不变性。因此没有必要再学习一个检测水平边界的卷积核了。

有时参数共享假设并没有意义。例如输入图像有明确的中心结构，这时我们希望在不同位置学习到不同特征。一个典型的例子就是人脸检测，人脸就位于图像中心位置，其他位置可能学到眼睛或头发特征；这种情况，就需要放松参数共享的限制，称这样的层叫做局部连接层Locallly-Connected Layer。

Numpy example，下面使用Numpy一个具体例子来说明，假设Numpy数组为X，

• 在深度上的某一列位置(x,y)，表示为X[x,y,:]。
• 在深度d上的一个切片，表示为X[:,:,d]。

假设输入X的形状X.shape:(11,11,4)。零填充P=0，滤波器核F=5，步长S=2，输出size为(11-5)/2+1=4,输出用V来表示：

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

其中，*表示逐个元素相乘，W0表示权重，b0表示偏置bias，W0大小W0.shape:(5,5,4)，5表示卷积核大小，4表示深度。计算在同一个深度切片时，使用的是同一个权重和bias，这就是参数共享。第二个特征图计算：

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1
• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1

上面是计算第二个特征图的过程。计算特征图后，往往跟着非线性操作例如ReLU，这里没有展示。

总结：

• 输入数据size:$W_1 \times H_1 \times D_1$
• 需要使用的超参数：
  1、卷积核个数$K$
  2、卷积核大小$F$
  3、步长$S$
  4、零填充大小$P$
• 输出大小size为$W_2 \times H_2 \times D_2$，其中
  $W_2 = (W_1 - F + 2P)/S + 1$
  $H_2 = (H_1 - F + 2P)/S + 1$
  $D_2 = K$

• 使用超参数共享，每个滤波器权重个数$F \cdot F \cdot D_1$，共有权重$(F \cdot F \cdot D_1) \cdot K$个，偏置$K$个。

• 输出中，在深度的第$d$个切片上（size为$W_2 \times H_2$），其结果是第$d$个卷积核与输入卷积的结果，卷积步长为$S$。

超参数的设置，习惯为$F = 3, S = 1, P = 1$。

卷积例子
因为3维数据难以可视化，下面图中，每一行是深度上的一个切片，输入时蓝色，权重是红色，输出是绿色。输入size$W_1 = 5, H_1 = 5, D_1 = 3$，卷积层参数$K=2,F=3,S=2,P=1$，即有2个$3 \times 3$的卷积核，步长为2，零填充为$P=1$。下面是动态示意图：

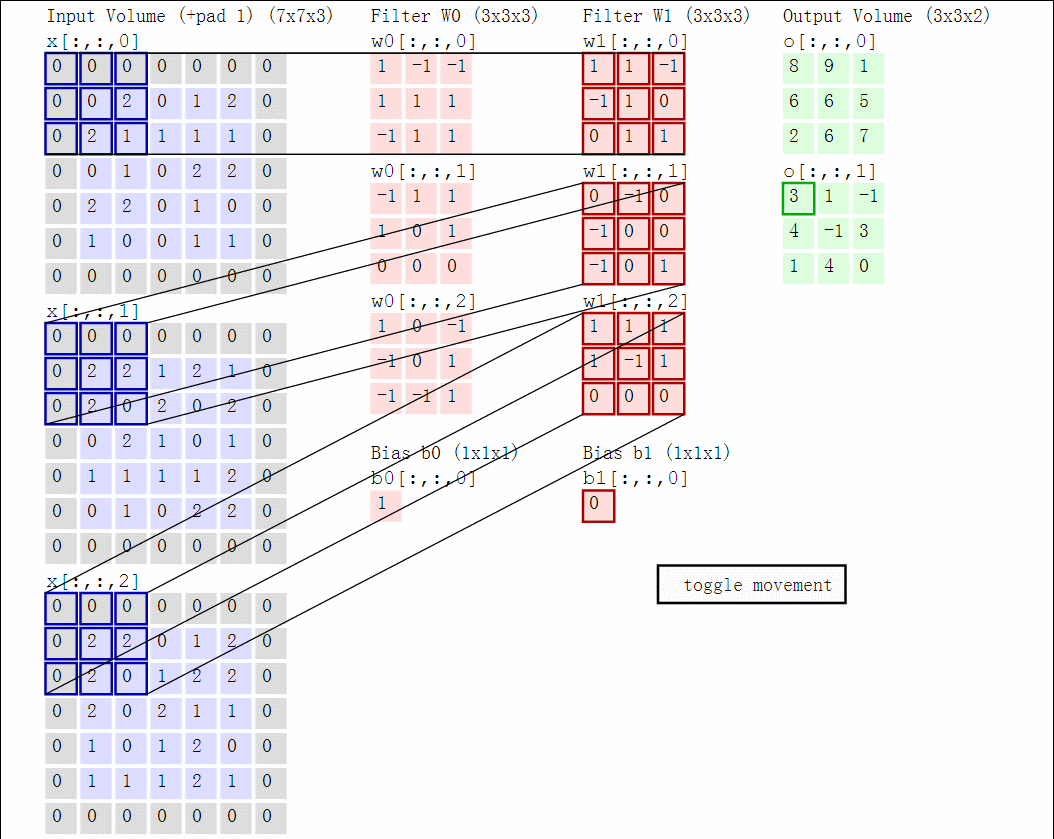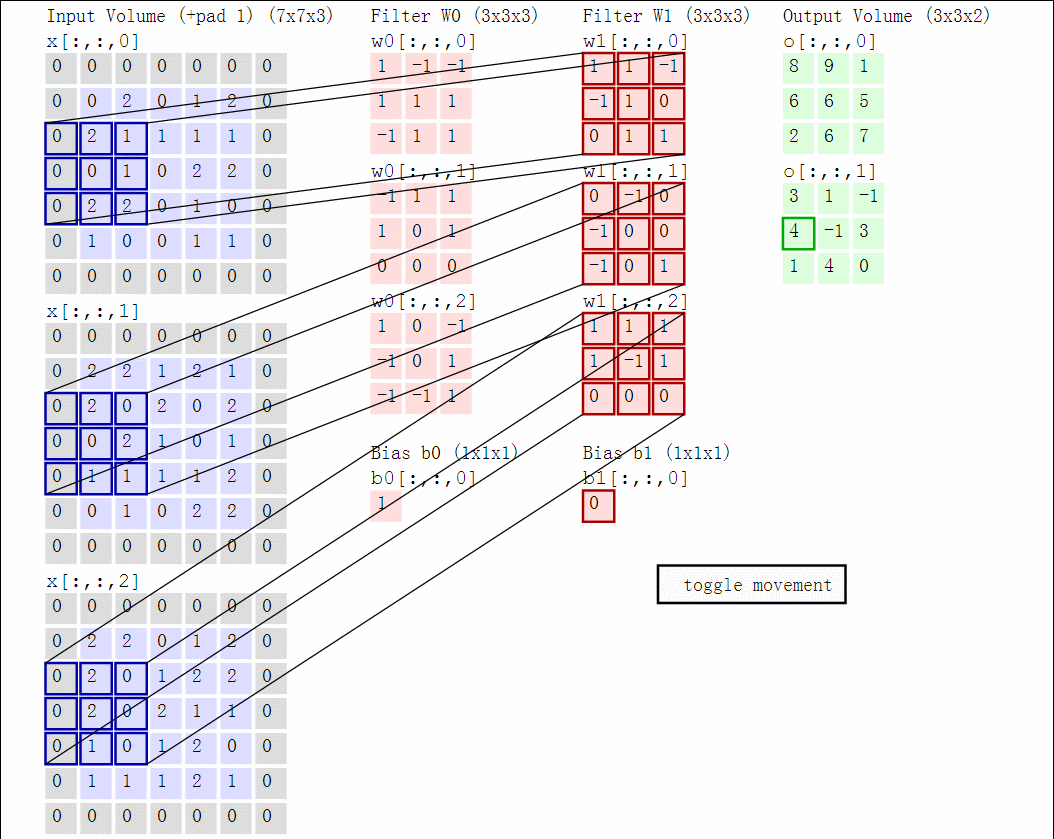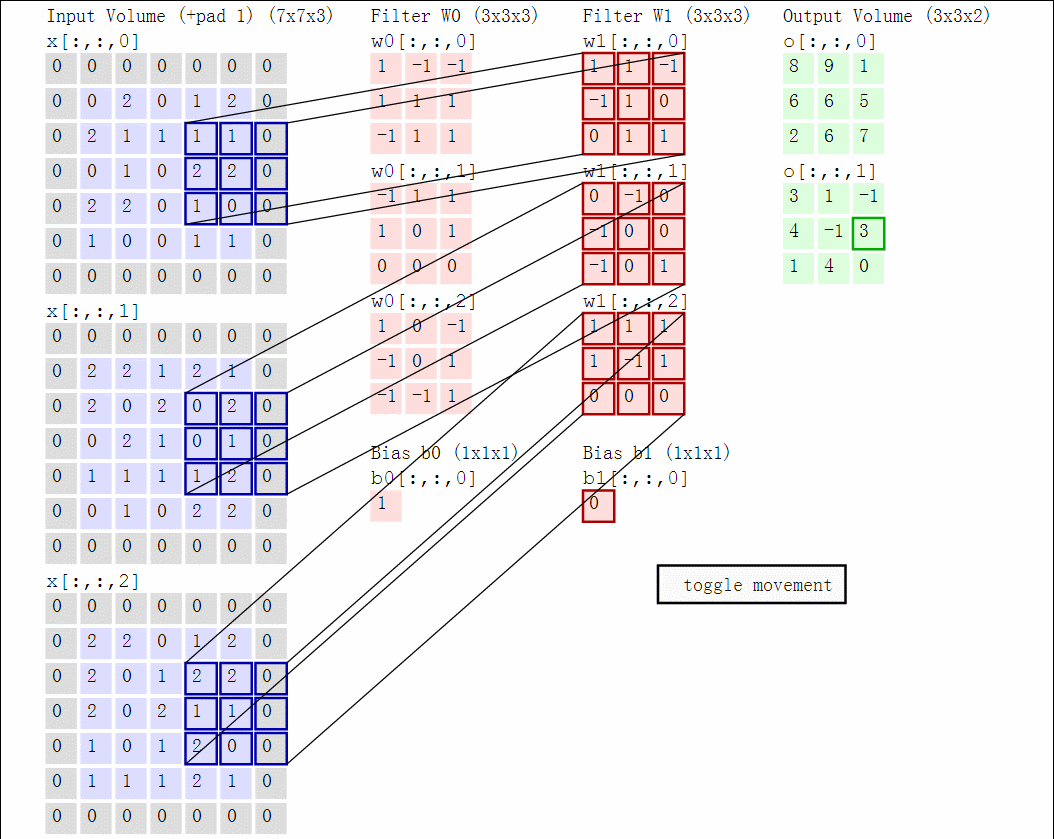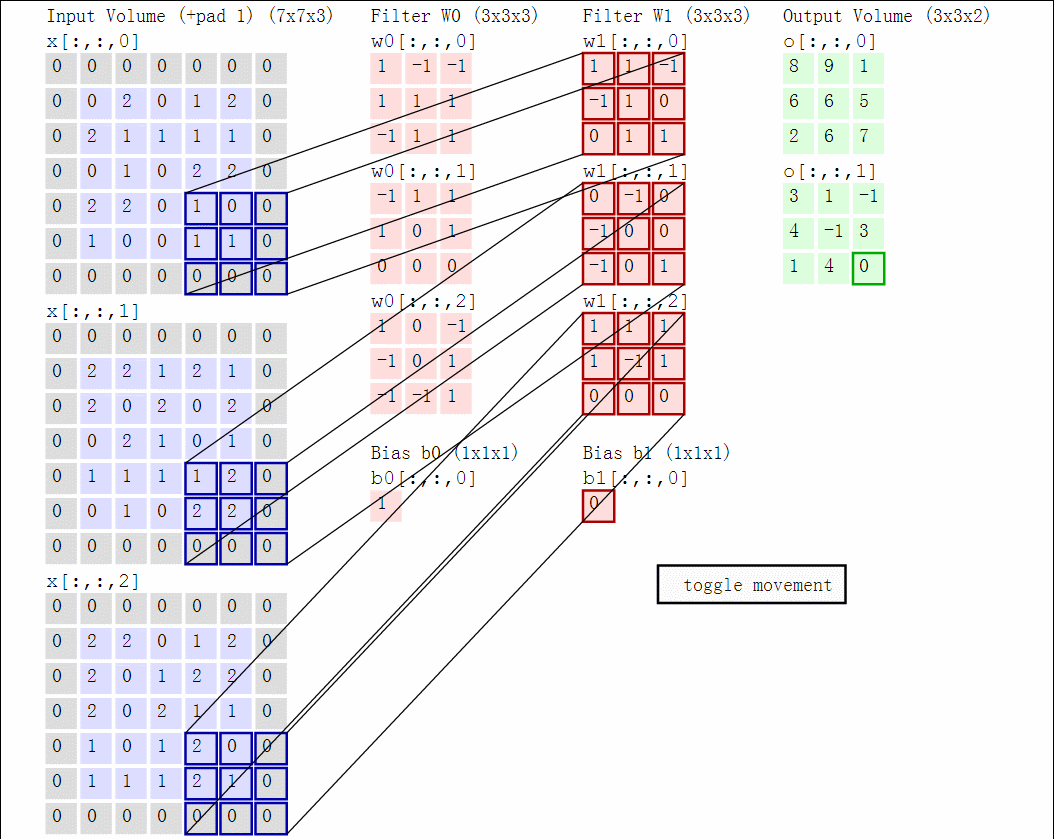
以矩阵乘积方式实现：
卷积操作是输入的局部区域和卷积核的点乘，可以利用这一点用一个大矩阵相乘来实现：
1、使用im2col操作，把输入的局部区域当做一列，展开为一个大矩阵。例如输入[227x227x3]，卷积核[11x11x3]，步长为4；从输入中取出[11x11x3]大小的块展开为一个列向量，列向量大小为11113=363。沿着步长为4来重复进行这个操作，在width和height方向分别迭代(227-11)/4+1=55次，共进行55*55=3025次。这样展开后矩阵X_col的size大小为[363x3025]，每一列是局部视野展开后的数据。注意局部视野有重叠，因此展开后的列可能会有重复。
2、卷积核的权重展开为行。例如96个[11x11x3]的卷积核，展开后的权重矩阵W_row大小为[96x363]。
3、卷积的结果为上面两个矩阵相乘np.dot(W_row,X_col)，相当于卷积核和感受视野的点乘。上面的例子中，得到结果为[96x3025]。
4、把得到的结果重新排列，正确的size为[55x55x96]。

这个方法的缺点是占用了过多内存，因为X_col中的数据有重复；优点是可以高效实用矩阵乘法（使用BLAS接口）。这个思想同样适用于pooling操作。

反向传播
卷积反向传播同样是卷积操作（对于数据和权重都是，但是在空间反转）。

1x1卷积
论文Network in Network首次发明了1x1卷积，信号处理背景的人可能疑惑。通常信号是2维数据，1x1卷积没有意义（只是缩放）。但是在卷积网络中，数据是3维的，滤波器深度和输入数据深度相同。例如输入[32x32x3]，使用1x1卷积，是3维的点乘。

扩展卷积
Fisher Yu and Vladlen Kultun的论文引入了另外一个超参数叫做扩张dilation。前面我们讨论的卷积核是连续的，同样卷积核之间也可以有间隔。例如size为3的卷积核计算输入为x，w[0]*x[0] + w[1]*x[1] + w[2]*x[2]，这是dilation为0的情况；如果dilation为1，那么计算为w[0]*x[0] + w[1]*x[2] + w[2]*x[4]。扩张卷积核正常卷积结合非常有用，例如可以在很少的层中汇聚到大尺度特征。使用2个3x3卷积，第二个卷积对输入数据的感受视野为5x5。可以看出如果使用扩展卷积，感受视野将迅速增长。

池化层

在卷积神经网络中，常常在连续卷积层中间隔插入池化层。池化操作可以减小数据量，从而减小参数，降低计算，因此防止过拟合。池化操作在每个深度切片上进行，例如使用MAX操作。常用的池化核实2x2大小，在每个深度切片的width和height方向下进行下采样，忽略掉75%（3/4）的激活信息。池化操作，保持深度depth大小不变。

池化层配置：

• 接收数据size $W_1 \times H_1 \times D_1$
• 需要参数
  1、池化核大小$F$
  2、步长$S$

• 输出数据大小$W_2 \times H_2 \times D_2$
  $W_2 = (W_1 - F) / S + 1$
  $H_2 = (H_1 - F) / S + 1$
  $D_2 = D_1$

• 池化层没有参数。

• 注意，在池化层一般不会使用零填充。

在实际使用中，最长见到的两种池化层配置：$F = 3, S = 2$（叫做重叠池化）；$F = 2, S = 2$，这个更常见。更大的池化核对网络有破坏性。

通用池化
除了MAX池化操作外，还有平均池化核L2-norm池化。平均池化在历史上用的比较多，现在渐渐被遗弃，因为和MAX池化相比，MAX池化往往性能更好。

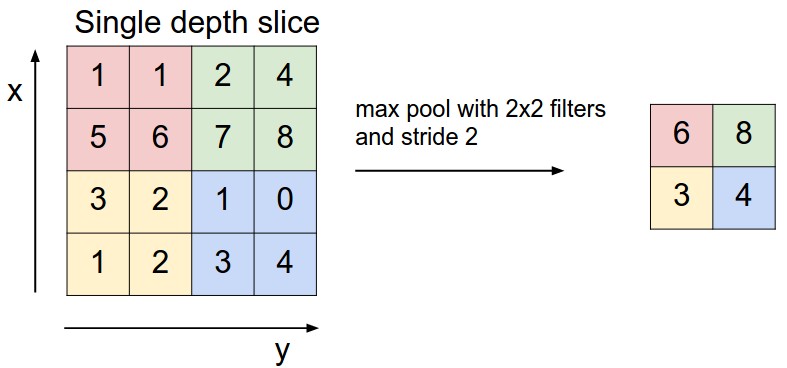
上图就是池化过程。左图输入为[224x224x64]，池化核[2x2]，输出为[112x112x64]；右图为池化具体计算过程，使用的是MAX池化。

反向传播
前面提到，对于max(x,y)的前向传播，只允许值大的通过；反向传播时只允许值大的输入的梯度反向传播。因此，池化层前向传播时记录下值大者的索引（有时叫做switches)，这样反向传播就很高效。

去掉池化
有些人不喜欢池化操作，可以考虑去掉池化层。例如Striving for Simplicity: The All Convolutional Net中全是重复的卷积层。为了降低数据大小，使用了大的步长。为了训练一个好的生成网络，可以去掉池化层，例如自编码（VAEs）或生成对抗网络（GANs：generative adversarial networks）。在未来的架构中，不使用池化层的可能性比较小。

归一化层

归一化层(Normalization Layer)是根据对大脑观察原理得来的。实践中有很多类型归一化层，但它们基本没有什么效果，即使有也微乎其微。因此逐渐被放弃。想了解归一化层，可以参考cuda-convnet library API.)

全连接层

如果一层的神经元和前一层的每个神经元都有连接，这样的层叫做全连接层。这样的层可以使用矩阵相乘再加上bias即可。

全连接层转为卷积层

全连接层和卷积层相似，卷积层的神经元和上一层输出局部区域相连接，使用了参数共享；因此它们之间可以相互转换。

• 一个卷积层，可以用一个全连接层来替换；替换后权重矩阵非常大，且大部分为零（因为卷积只是局部连接），权重矩阵中很多块相同（因为参数共享）。

• 全连接层可以转换为卷积层。例如对于一个全连接层$K = 4096$,输入为$7 \times 7 \times 512$，可以转换为卷积层$F = 7, P = 0, S = 1, K = 4096$，即卷积核和输入大小相同，输出变为$1 \times 1 \times 4096$。

FC->CONV
在实践中，全连接层转换为卷积层更为有用。AlexNet输入为224x224x3，通过一系列卷积池化层，得到7x7x512输出(224/2/2/2/2/2=7)，之后通过2个大小为4096的全连接层，最后通过1000个神经元的全连接层计算出每类别的得分。可以替换掉3个全连接层为3个卷积层：

• 替换掉第一个全连接层，其输入为[7x7x512]，替换用的卷积核$F = 7$，输出为[1x1x4096]。
• 替换掉第二个全连接层，其输入为[1x1x4096]，替换用的卷积核$F = 1$，输出为[1x1x4096]。
• 替换掉第三个全连接层，其输入为[1x1x4096]，替换用的卷积核$F = 1$，输出为[1x1x1000]。

上面这些转换操作，涉及到重塑（例如reshape）权重矩阵$W$。这样在单一前向传播中，可以更高效；因为当输入图像比较大时，可以沿着额外空间滑动。

例如AlexNet[224x224x3]输入，输出[7x7x512]，长和宽减小2x2x2x2x2=32倍；如果输入为[384x384x3]，那么输出为[12x12x512]，因为384/2/2/2/2/2=12。后面跟着的三个卷积层，最后得到输出为[6x6x1000]，因为(12 - 7) / 1 + 1 = 6。之前输出为[1x1x1000]对应一个类别一个得分，现在为结果为[6x6x1000]。不把全连接层替换为卷积层，输入为[384x384x3]，使用[224x224]窗口，步长为32滑动，得到6x6个[224x224x3]图像，最终结果也是[6x6x1000]。

上面两种方法得到结果一样，显然前一种效率更高。这样的计算技巧在实践中常常使用；例如把小图像resize更大，使用转换后的卷积网络，计算多个位置得分，最终取平均值。

如果我们想使用的步长小于32，可以使用多次前向传播。第一次使用原图前向传播；第二次使用步长16沿着宽和高平移，把平移后的图片输入到网络计算。

• IPython Notebook例子Net Surgery展示如何使用Caffe实践转换。

卷积网络架构

卷积网络通常由CONV,POOL,FC三种类型的层组成，其中POOL默认为Max pool；RELU也显式指出。下面讨论怎么组合这些层。

层模式

最常见的模式是连续几个CONV-RELU，后面跟着一个POOL；重复这样的结构几次，直到输出比较小，在某一位置使用FC。最后一个FC输出结果，例如类别得分。即常见的模式为：

INPUT->[[CONV->RELU]*N]->POOL?]*M->[FC->RELU]*K->FC

其中*表示重复，POOL?表示可选；一般N >= 0（通常N <= 3）, M >= 0, K >= 0(通常K < 3)。例如一些常见的卷积网络架构模式如下：

• INPUT->FC，实现的是一个线性分类器，这里N=M=K=0。
• INPUT->CONV->RELU->FC。
• `INPUT->[CONV->RELU->POOL]*2->FC->RELU->FC，在每个CONV后面有一个POOL。
• INPUT->[CONV->RELU->CONV->RELU->POOL]*3->[FC->RELU]*2->FC，这里每2个CONV后面有一个POOL，这样的结构在大的深度网络常常见到，在POOL层破坏特征前，连续多个CONV层可以提取更复杂的特征。

宁愿使用连续多个小的滤波器，不使用一个大的滤波器。例如连续3个CONV，每层滤波器核大小都是3x3。第一层CONV对于INPUT感受视野是3x3，第二层CONV对于INPUT感受视野是5x5，第三层对于INPUT的感受视野是7x7；如果换用一层CONV，核大小为7x7，将会有以下缺点：1、一层对于输入来说是线性计算，三层具有很好的非线性，具有更强的表达能力。2、假设channel数为$C$，对于一层7x7卷积层，共有权重$C \times (7 \times 7 \times C) = 49C^2$，而三层3x3卷积，共有参数$3 \times (C \times (3 \times 3 \times C)) = 27C^2$。可以看出，连续的小卷积核，具有更少的参数和更强的表达能力；但是连续小的卷积核在训练时占用更多内存，因为在反向传播时需要用到中间结果。

最新进展
上面提到的按照组合组成卷积网络方法已经收到挑战。来自Google的Inception结构和来自微软的Residual Networks没有按照上面方法设计网络结果；它们设计更加复杂。

实战经验：使用在ImageNet上效果好的任何方法
90%的应用不需要过多思考如何设计网络架构。”don’t be a hero”:不是不断设计变换你自己的网络架构，你需要查看任何能在ImageNet挑战赛上表现性能好的网络，下载预训练模型，用自己数据finetune。很少情况需要你从头训练和设计，在Deep Learning school我也强调了这一点。

层大小设计模式

到现在为止还没提及层中常规超参数；下面将先介绍这些超参数设计准则，然后来讨论：

输入层INPUT包含图像，其大小一般可以连续整除多个2。常见的包括32（CIFAR-10）,64,96(STL-10),224,384,512。

卷积层CONV使用核小的滤波器（3x3，最多5x5），步长$S=1$；如果输入输出height和width保持不变，那么使用零填充$P=(F-1)/2$。如果必须使用大的卷积核（例如7x7），通常在第一层使用。

池化层POOL是对输入数据在height和width上的下采样，最常见的下采样max-pooling，$F=2,S=2$，这样将会丢掉75%激活信息。还有一个也比较常见的，$F=3,S=2$。更大的池化层很少见，因为池化层会丢弃特征，太大的池化层影响性能。

减少尺寸设计的问题
前面设计中，CONV输入输出heigh和width不变；如果步长大于1或不使用零填充，那么CONV也将会引起height和width减小，这时需要认真设计，确保数据和核大小匹配。

为什么CONV中步长为1
在实践中，小步长效果更好。使用步长为1，输入输出在卷积空间大小保持不变，这样只有在POOL中下采样才会引起空间尺寸减小。

为什么使用padding
在CONV使用padding，可以保持输入输出空间维度尺寸不变，也可以提升性能。如果在CONV不使用padding，经过CONV后，数据空间维度尺寸会略微减小，这样图像的边缘信息将会很快丢失掉。

基于内存限制的妥协
卷积网络中，内存消耗很快，且会限制卷积网络。例如输入[224x224x3]的图像，使用64个3x3大小滤波器，零填充$P=1$，则输出为[224x224x64]。这个数量，将会有1千万激活，占用72M内存（每张图像，对于激活和梯度都是）。因为GPU显存的限制，常常要做出妥协；实践中，常常在第一层做出妥协，例如ZFnet第一层卷积核7x7，步长为2,AlexNet第一层卷积核7x7，步长为4。

实例

卷积网络中有几个经典网络：

• LeNet，第一个成功的卷积网络，由Yann LeCun在九十年代发明。最出名的是它的架构，已经应用到邮政编码和数字识别。

• AlexNet，第一个在机器视觉领域留下的网络，由Alex Krizhevsky, Ilya Sutskever and Geoff Hinton发明，赢得了2012年的 ImageNet ILSVRC challenge，识别率远远超过第二名（top 5 错误了16%，第二名为26%）。AlexNet类似LeNet，但是更深更广，使用了连续的CONV（之前都是CONV后跟着POOL）。

• ZF Net，2013年ILSVR冠军，由Zeiler和Rob Fergus发明，ZF Net是他们名字缩写。ZF Net是基于AlexNet微调而来，扩大了中间卷积层的尺寸，减小了第一个卷积层的核和步长。

• GoogLeNet,2014年ILSVR冠军，来自Google，由Szegedy et al发明。它的主要贡献在于发展了Inception结构，Inception架构可以减小参数个数（只有4M，相比AlexNet有60M）。它还在卷积层顶部使用平均池化层替代全连接层，减小了许多不重要的参数。后续还有几个版本，最新的为inception-V4。

• VGGNet，2014年ILSVRC的亚军是Simonyan and Andrew Zisserman发明的VGGNet。VGGNet向我们证明了深度对于卷积网络的重要性。最终性能最优的网络是16层CONV/POOL，从输入到输出层结构相同，都是3x3卷积核2x2池化。预训练模型可以在caffe上直接使用。VGGNet缺点是非常耗计算资源和内存，它有140M参数。大部分参数在第一个全连接层，后来发现它可以移去，且性能几乎不会有影响，因此减少了参数个数。

• ResNet，Residual Network由He等发明，赢得了2015 ILSVRC冠军。它的特点是使用了跳跃连接，大量使用了batch normalization。ResNet在网络的末端没有使用全连接层；可以参考Kaiming的报告(videoslides)。它是目前（2016-05-10）最好的卷积网络。可以参考最近最这个网络的优化Kaiming He et al. Identity Mappings in Deep Residual Networks (2016-03发表）。

详细分析VGGNet
以VGGNet为例，详细分解。VGGNet由卷积层(核3x3，步长1，零填充1）和池化层（2x2max池化，步长2，没有零填充）。下面分解每一层的大小，并记录每层权重个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

INPUT:[224x224x3]    memory:224x224x3=150k    weights:0
CONV3-64:[224x224x64]    memory:224x224x64=3.2M    weights:(3*3*3)*64=1,728
CONV3-64:[224x224x64]    memory:224x224x64=3.2M    weights:(3*3*64)*64=36,864
POOL2: [112x112x64]  memory:  112*112*64=800K   weights: 0
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128]  memory:  56*56*128=400K   weights: 0
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256]  memory:  28*28*256=200K   weights: 0
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512]  memory:  14*14*512=100K   weights: 0
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512]  memory:  7*7*512=25K  weights: 0
FC: [1x1x4096]  memory:  4096  weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096]  memory:  4096  weights: 4096*4096 = 16,777,216
FC: [1x1x1000]  memory:  1000 weights: 4096*1000 = 4,096,000

TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parameters

通常来说，卷积网络中，最前面几个卷积层占用了大部分内存，第一个全连接层占用了大部分参数。在这个例子中，第一个卷积层包含100M参数，参数总个数才140M。

计算资源考虑

卷积网络最大限制在于内存，GPU内存一般为3/4/6G，当前最好的GPU大概有12G。有三种主要占用内存的来源：

• 中间数据。每个卷积层都有激活的原始数据和梯度（它们大小相同），大部分的激活数据在前面几个卷积层中；要记录它们是因为在反向传播时需要使用。但是在测试时就可以释放前面激活层数据占用的内存。

• 参数。网络中有大量参数，反向传播时它们的梯度，如果使用momentum,Adagrad,RMSProp还要记录一步缓存，所以参数存储空间要在最原始基础上乘以3甚至更多。

• 卷积网络实现。实现还要占用各种混杂（miscellaneous）内存，例如图像批数据，它们的扩展数据等。

对参数（激活、梯度、混杂）个数有了大概估计后，应该转换为GB单位。单精度乘以4，双精度乘以8，得到占用字节数；最终换算成GB。如果占用内存过多，最简单办法是减小batch size；因为大部分内存是被激活数据占用。

额外资源

这些资源涉及到实现：

• Soumith benchmarks for CONV performance
• ConvNetJS CIFAR-10 demo在浏览器实时查看计算结果。
• caffe一个流行的卷积网络库。
• ResNet Torch7实现。