机器学习常常转换为最优化问题。最优化问题往往没有闭式解,一般使用梯度下降法求解。梯度下降法需要用微分求梯度,自动微分是各个机器学习框架都支持的。
微分分类
求解梯度有以下方法:
- 数值求解
- 符号求解
- 自动求解
数值求解
数值求解是通过差分法是通过数值计算,通过有限差分无限逼近导数
$$
\frac{\partial f(x)}{\partial x} \approx lim_{h \to 0} \frac{f(x + h) - f(x - h)}{2h}
$$
上面求解只是近似导数;通过泰勒级数可以知道随着$h$减小,不断逼近真实导数。这个方法可以用来检验梯度是否正确,这时$h$取值通常为$1e-6$
符号求解
运算符可以求微分,例如$f(x) = 1 + 2x + 3x^2$,那么可以直接求得:
$$
\frac{\partial f(x)}{\partial x} = 2 + 3x
$$
一些复杂的运算可以通过链式法则,例如
$$\frac{d(f+g)}{dx} = \frac{df}{dx} + \frac{dg}{dx} $$
$$\frac{d(fg)}{dx} = \frac{df}{dx}g + f \frac{dg}{dx}$$
$$\frac{d(h(x))}{dx} = \frac{df(g(x))}{dg(x)} \cdot \frac{dg(x)}{dx}$$
符号微分没有误差,但是随着计算表示式变得复杂,微分表达式的复杂度会呈指数增长;有时只是想拿到一个微分的数值结果,使用符号求解会保留太多的中间符号表达式。
自动微分
自动微分是数值求解和符号求解的结合。数值求解是带入数值进行计算,符号求解是通过链式法则求解微分表达式,之后带入数值计算。
自动微分法是通过符号求解求得微分表达式,之后立刻带入数值进行计算,保留中间结果;将这样的方法应用到整个函数表达式即可。
Forward mode和Backward mode
在说明Forward和Backward之前,先了解一下计算图
计算图
计算图是把有依赖关系的计算表达式按照拓扑排序组成的图形结构。例如$e = (a + b) (b + 1)$,可以分成一下运算
$$c = a + b$$
$$d = b + 1$$
$$e = c d$$
上述计算构建成计算图: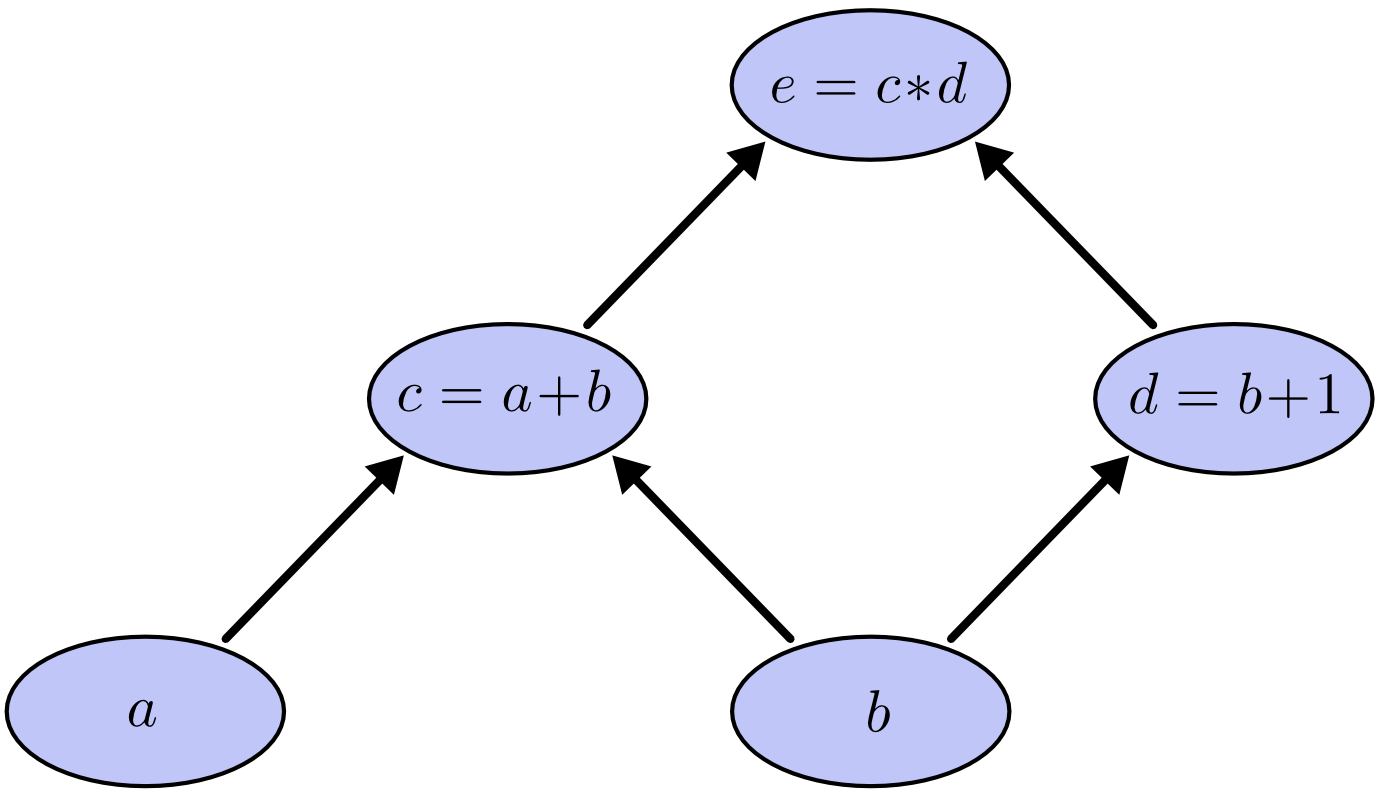
图中的有向边表示依赖关系,结点表示输入/输出/中间结果,结点还带有一个操作符(输入结点的操作是赋值)。计算表达式只需要按照计算图从下向上计算即可。
Forward和Backward是指计算导数的方式。计算表示式结果只有Forward模式,但是计算导数有两种方式。
Forward mode和Backward mode
所谓Forward mode和Backward mode是指计算导数时,是从下往上还是从上往下。例如根据计算求得每个边的导数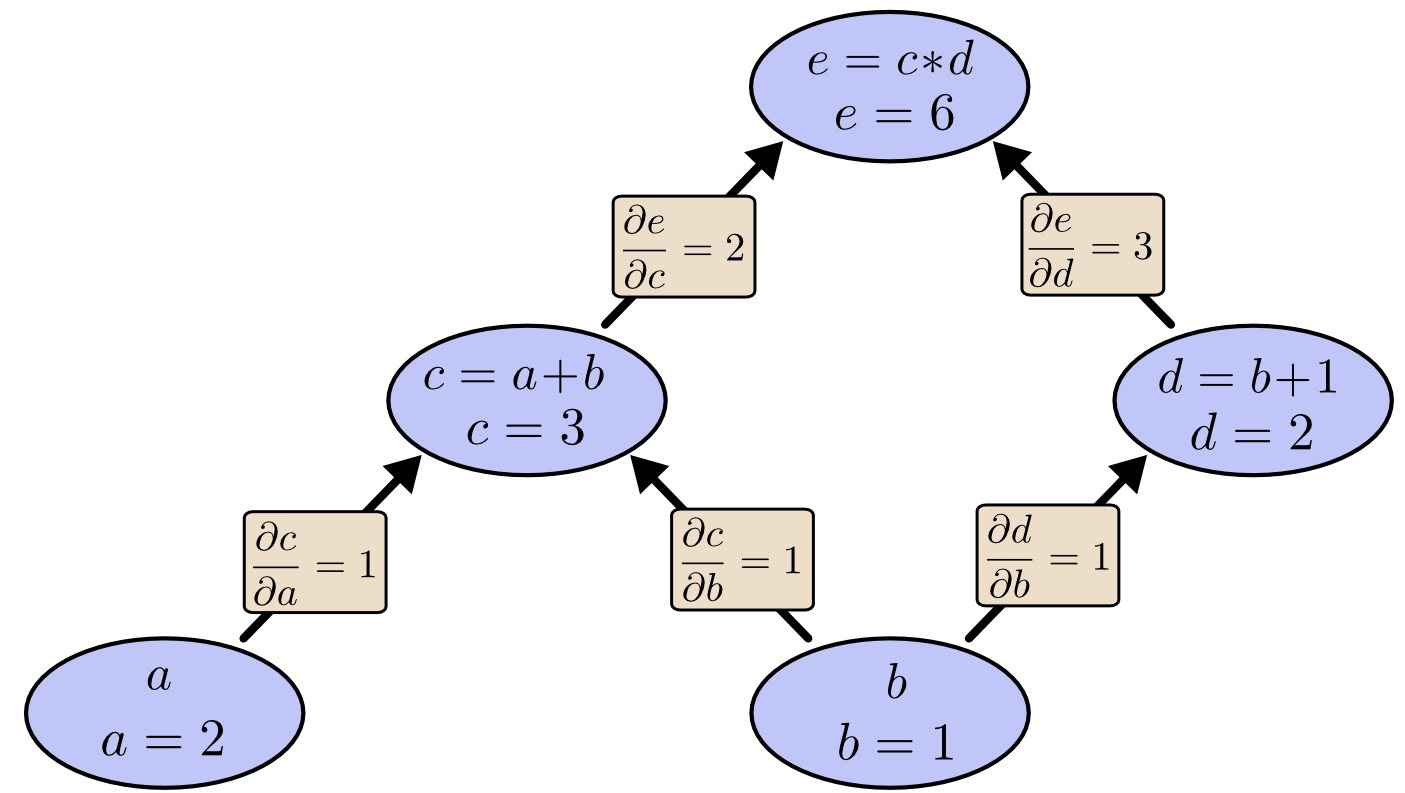
计算$\frac{\partial e}{\partial b}$的Forward mode
$$
\frac{\partial e}{\partial b} = \frac{\partial c}{ \partial b} \frac{\partial e}{\partial c} + \frac{\partial d}{ \partial b} \frac{\partial e}{\partial d} = 1 2 + 1 3 = 5
$$
计算$\frac{\partial e}{\partial b}$的Backward mode
$$
\frac{\partial e}{\partial b} = \frac{\partial e}{\partial c} \frac{\partial c}{ \partial b} + \frac{\partial e}{\partial d} \frac{\partial d}{ \partial b} = 2 1 + 3 1 = 5
$$
Forward mode和计算表达式结果顺序一致,Back ward是从结果向前运算。
在DL中,要求解的导数不止一个,如果使用Forward mode,那么中间结果将不可重复使用,且会有大量重复计算;因为DL使用Backward mode计算导数。
自动微分
自动微分是把计算图上的微分表达式求解出来,形成求解微分的计算图。按照计算图求解即可。1
2
3
4
5
6def gradient(out):
node_to_grad[out] = 1
for node in reverser_topo_order(out):
grad <- sum partial adjoints from output edges
input_grads <- calc partial adjoints for inputs given node.op and grad
add input_grads to node_to_grad
首先求输出对自己的导数(数值是1)作为微分计算图的输入,这样求解微分的计算图。计算引擎负责计算和求解微分,使用Python实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75class Executor:
"""Executor computes values for a given subset of nodes in a computation graph."""
def __init__(self, eval_node_list):
"""
Parameters
----------
eval_node_list: list of nodes whose values need to be computed.
"""
self.eval_node_list = eval_node_list
def run(self, feed_dict):
"""Computes values of nodes in eval_node_list given computation graph.
Parameters
----------
feed_dict: list of variable nodes whose values are supplied by user.
Returns
-------
A list of values for nodes in eval_node_list.
"""
node_to_val_map = dict(feed_dict)
# Traverse graph in topological sort order and compute values for all nodes.
topo_order = find_topo_sort(self.eval_node_list)
"""TODO: Your code here"""
for node in topo_order:
if isinstance(node.op, PlaceholderOp):
continue
input_vals = [node_to_val_map[input_node] for input_node in node.inputs]
node_val = node.op.compute(node, input_vals)
node_to_val_map[node] = node_val if isinstance(node_val, np.ndarray) else np.array(node_val)
# Collect node values.
node_val_results = [node_to_val_map[node] for node in self.eval_node_list]
return node_val_results
def gradients(output_node, node_list):
"""Take gradient of output node with respect to each node in node_list.
Parameters
----------
output_node: output node that we are taking derivative of.
node_list: list of nodes that we are taking derivative wrt.
Returns
-------
A list of gradient values, one for each node in node_list respectively.
"""
# a map from node to a list of gradient contributions from each output node
node_to_output_grads_list = {}
# Special note on initializing gradient of output_node as oneslike_op(output_node):
# We are really taking a derivative of the scalar reduce_sum(output_node)
# instead of the vector output_node. But this is the common case for loss function.
node_to_output_grads_list[output_node] = [oneslike_op(output_node)]
# a map from node to the gradient of that node
node_to_output_grad = {}
# Traverse graph in reverse topological order given the output_node that we are taking gradient wrt.
reverse_topo_order = reversed(find_topo_sort([output_node]))
"""TODO: Your code here"""
for node in reverse_topo_order:
grad = sum_node_list(node_to_output_grads_list[node])
node_to_output_grad[node] = grad
grads = node.op.gradient(node, grad)
if not grads:
continue
for one_input, one_grad in zip(node.inputs, grads):
if one_input not in node_to_output_grads_list:
node_to_output_grads_list[one_input] = []
node_to_output_grads_list[one_input].append(one_grad)
# Collect results for gradients requested.
grad_node_list = [node_to_output_grad[node] for node in node_list]
return grad_node_list
求解计算图过程比较简单,按照拓扑排序依次计算Node的数值即可。求解微分计算图稍微复杂一点;node_to_output_grad的key是Node结点,value是计算微分的表达式,如果一个node有多条计算路径到达结果Node结点,那么这个Node结点的微分表达式是这些路径求导的和;因此也就有了node_to_output_grads_list,它的key是node,value是个list,如果有多条路径,那么list包含各个路径求导的表达式。
参考
Calculus on Computational Graphs: Backpropagation
Lecture 4: Automatic Differentiation
Assignment 1: Reverse-mode Automatic Differentiation